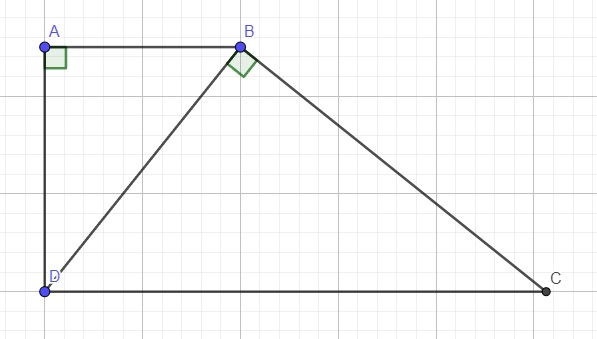
Cho hình thang vuông ABCD ( góc A=góc D=90o), có 2 đường chéo vuông góc với nhau. Chứng minh rằn AD2= AB.CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
Lời giải:
a. $BD\perp BC, BD=BC$ nên tam giác $BDC$ vuông cân tại $B$
$\Rightarrow \widehat{C}=45^0$
$\widehat{ABC}=180^0-\widehat{C}=180^0-45^0=135^0$
b.
Ta có: $\widehat{ABD}=\widehat{ABC}-\widehat{DBC}=135^0-90^0=45^0$ nên tam giác $ABD$ vuông cân tại $A$
$\Rightarrow AD=AB=3$
Áp dụng định lý Pitago:
$BD=\sqrt{AB^2+AD^2}=\sqr{3^2+3^2}=3\sqrt{2}$ (cm)
$BC=BD=3\sqrt{2}$ (cm)
Tam giác $BDC$ vuông cân tại $B$ nên áp dụng định lý Pitago:
$DC=\sqrt{BC^2+BD^2}=\sqrt{(3\sqrt{2})^2+(3\sqrt{2})^2}=6$ (cm)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2023
Ta có \(\Delta BCD\) vuông tại B nên \(\widehat{ADB}=\widehat{BCD}\) (cùng phụ \(\widehat{BDC}\))
Xét hai tam giác BAD và DBC có:
\(\left\{{}\begin{matrix}\widehat{ADB}=\widehat{BCD}\\\widehat{DAB}=\widehat{CBD}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta BAD\sim\Delta DBC\left(g.g\right)\)
\(\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{BD}\Rightarrow BD^2=AB.DC\)
