 vẽ hình có gt /kl
vẽ hình có gt /kl
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



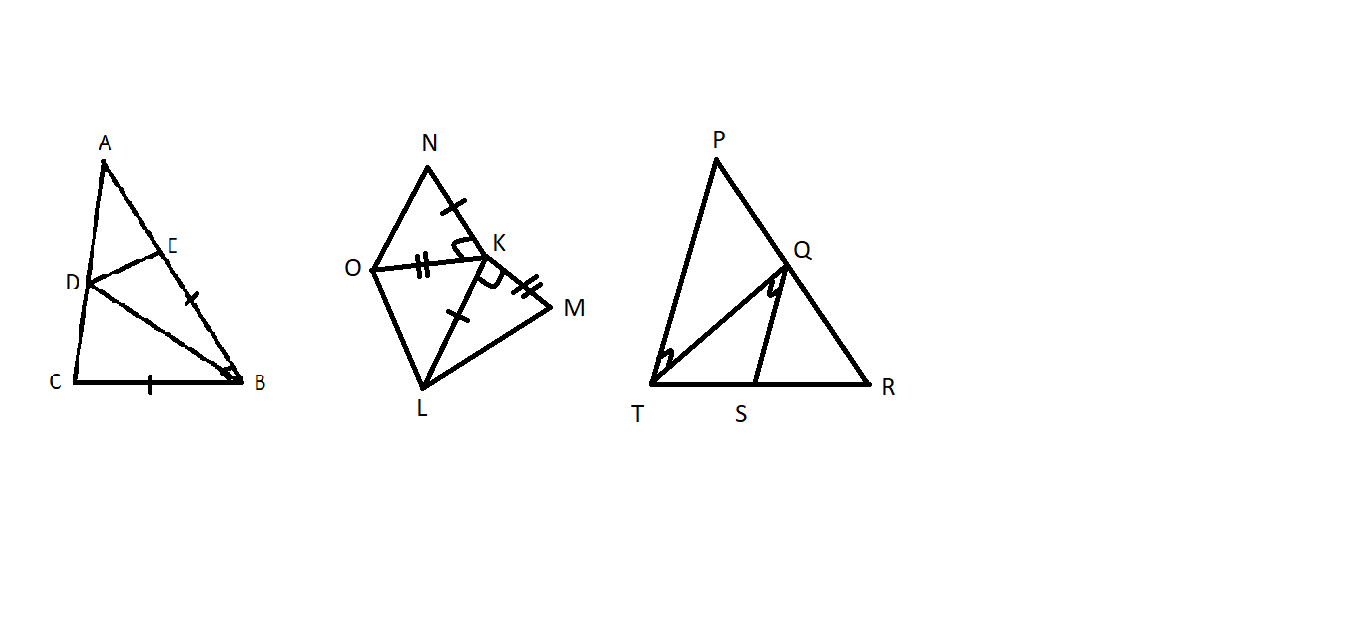
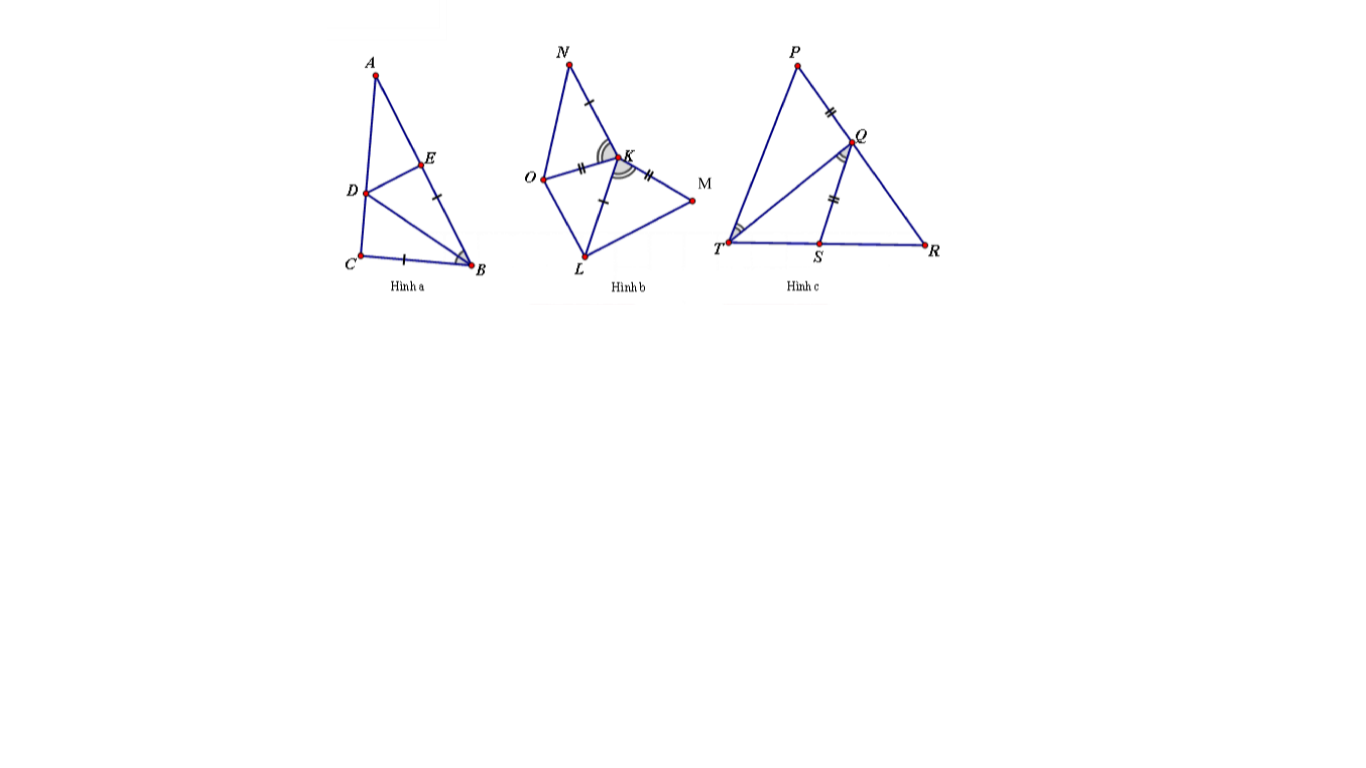
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM


a: Xét ΔOAH vuông tại A và ΔOBH vuông tại B có
OH chung
\(\widehat{AOH}=\widehat{BOH}\)
Do đó: ΔOAH=ΔOBH
Suy ra: OA=OB; AH=BH
b: Xét ΔBHE vuông tại B và ΔAHM vuông tại A có
HB=HA
\(\widehat{BHE}=\widehat{AHM}\)
Do đó: ΔBHE=ΔAHM
Suy ra: HE=HM
c: Ta có: OM=OE
nên O nằm trên đường trung trực của ME(1)
Ta có: HE=HM
nên H nằm trên đường trung trực của ME(2)
Từ (1) và (2) suy ra OH là đường trung trực của ME

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED

a: Xét tứ giác EFBC có
A là trung điểm của EB
A là trung điểm của CF
Do đó: EFBC là hình bình hành
Suy ra: EF=BC

1. Xét tam giác ABD và tam giác AED có:
\(\text{+}\) AD chung.
\(\text{+}\) \(\widehat{BAD}=\widehat{EAD}\) (AD là phân giác).
\(\text{+}\) AB = AE (gt).
\(\Rightarrow\) Tam giác ABD = Tam giác AED (c - g - c).
2. a) Tam giác ABD = Tam giác AED (cmt).
\(\Rightarrow\) \(\widehat{ABD}=\widehat{AED}\) (2 góc tương ứng).
Mà \(\widehat{ABD}+\widehat{KBD}=\)\(180^o.\)
\(\widehat{AED}+\widehat{CED}=\)\(180^o.\)
\(\Rightarrow\) \(\widehat{KBD}=\widehat{CED} (đpcm).\)
b) Xét tam giác KBD và tam giác CED có:
\(\text{+}\) \(\widehat{KBD}=\widehat{CED} \) (cmt).
\(\text{+}\) BD = ED (Tam giác ABD = Tam giác AED).
\(\text{+}\) \(\widehat{BDK}=\widehat{EDC}\) (2 góc đối đỉnh).
\(\Rightarrow\) Tam giác KBD = Tam giác CED (g - c - g).
3. Ta có: KE = KD + DE; CB = CD + DB.
Mà KD = CD (Tam giác KBD = Tam giác CED).
DE = DB (Tam giác ABD = Tam giác AED).
\(\Rightarrow\) KE = CB.
Xét tam giác KBE và tam giác CEB có:
\(\text{+}\) KE = CB (cmt).
\(\text{+}\) BK = EC (Tam giác KBD = Tam giác CED).
\(\text{+}\) BE chung.
\(\Rightarrow\) Tam giác KBE = Tam giác CEB (c - c - c).
4. Ta có: DE \(\perp\) AC (gt). => Tam giác AED vuông tại E.
Mà tam giác ABD = tam giác AED (cmt).
\(\Rightarrow\) Tam giác ABD vuông tại B.
\(\Rightarrow\) \(\widehat{ABD}\) \(=90^o.\)
\(\Rightarrow\) Tam giác ABC vuông tại B.
Vậy để DE \(\perp\) AC thì tam giác ABC vuông tại B.


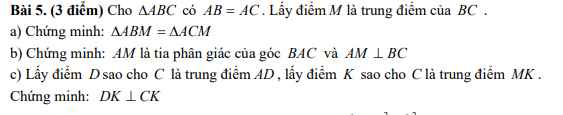
 Vẽ hình ghi gt và kl giúp em luôn nha
Vẽ hình ghi gt và kl giúp em luôn nha

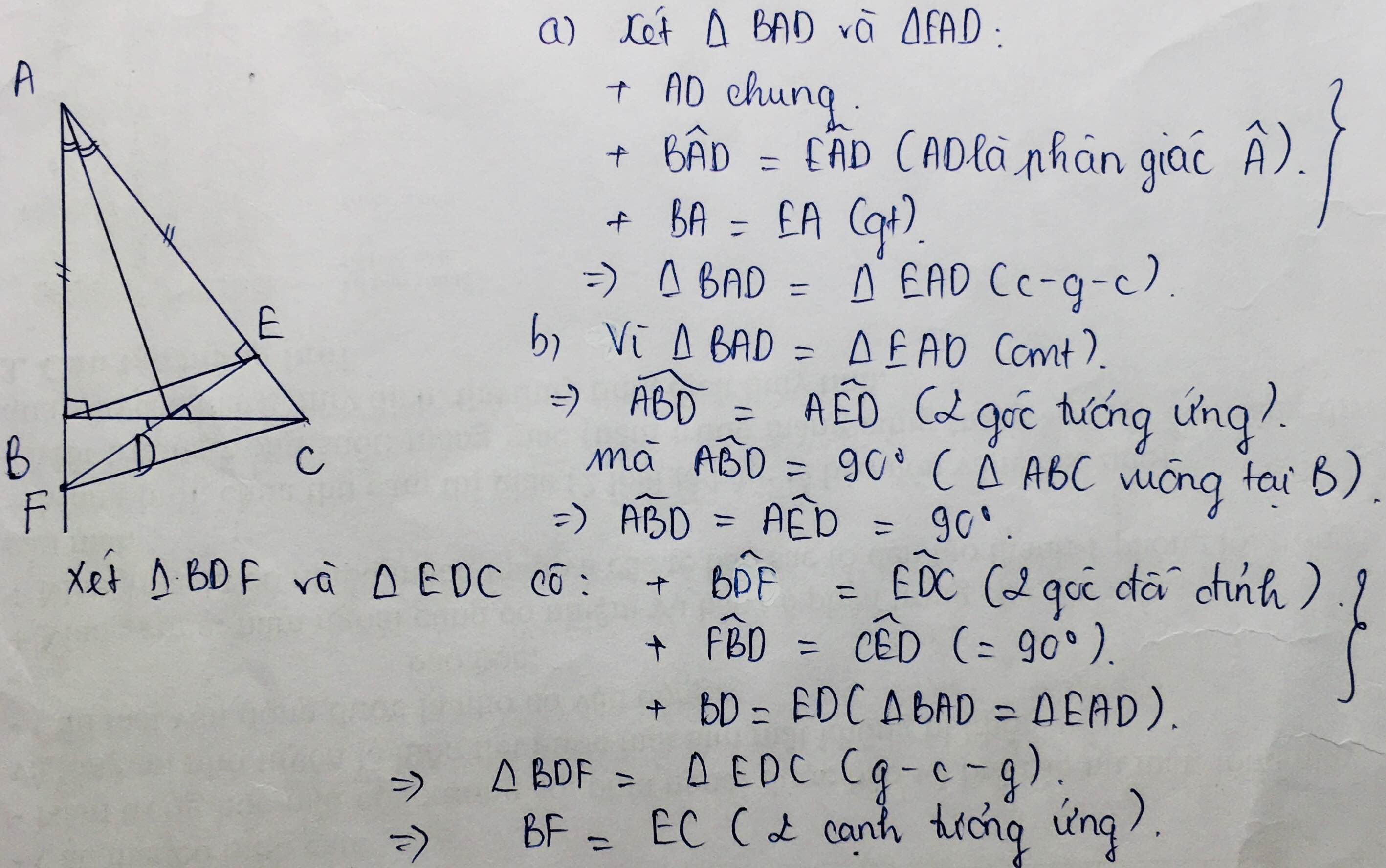



a: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>PA\(\perp\)BD tại A
Xét (O) có
ΔCIB nội tiếp
CB là đường kính
Do đó: ΔCIB vuông tại I
Xét tứ giác ADHC có \(\widehat{DAC}+\widehat{DHC}=90^0+90^0=180^0\)
nên ADHC là tứ giác nội tiếp
b: Xét ΔDBP có
PA,BH là các đường cao
PA cắt BH tại C
Do đó: C là trực tâm của ΔDBP
=>DC\(\perp\)BP
mà CI\(\perp\)BP
mà DC,CI có điểm chung là C
nên D,C,I thẳng hàng
(O) có đường kính BC
\(A\in\left(O\right);AP>AC;P\in AC\)
PB\(\cap\)(O)={I}
PH\(\perp\)BC tại H, PH cắt BA tại D
a: ACHD nội tiếp
b: D,C,I thẳng hàng