Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
1. Xét tam giác ABD và tam giác AED có:
\(\text{+}\) AD chung.
\(\text{+}\) \(\widehat{BAD}=\widehat{EAD}\) (AD là phân giác).
\(\text{+}\) AB = AE (gt).
\(\Rightarrow\) Tam giác ABD = Tam giác AED (c - g - c).
2. a) Tam giác ABD = Tam giác AED (cmt).
\(\Rightarrow\) \(\widehat{ABD}=\widehat{AED}\) (2 góc tương ứng).
Mà \(\widehat{ABD}+\widehat{KBD}=\)\(180^o.\)
\(\widehat{AED}+\widehat{CED}=\)\(180^o.\)
\(\Rightarrow\) \(\widehat{KBD}=\widehat{CED} (đpcm).\)
b) Xét tam giác KBD và tam giác CED có:
\(\text{+}\) \(\widehat{KBD}=\widehat{CED} \) (cmt).
\(\text{+}\) BD = ED (Tam giác ABD = Tam giác AED).
\(\text{+}\) \(\widehat{BDK}=\widehat{EDC}\) (2 góc đối đỉnh).
\(\Rightarrow\) Tam giác KBD = Tam giác CED (g - c - g).
3. Ta có: KE = KD + DE; CB = CD + DB.
Mà KD = CD (Tam giác KBD = Tam giác CED).
DE = DB (Tam giác ABD = Tam giác AED).
\(\Rightarrow\) KE = CB.
Xét tam giác KBE và tam giác CEB có:
\(\text{+}\) KE = CB (cmt).
\(\text{+}\) BK = EC (Tam giác KBD = Tam giác CED).
\(\text{+}\) BE chung.
\(\Rightarrow\) Tam giác KBE = Tam giác CEB (c - c - c).
4. Ta có: DE \(\perp\) AC (gt). => Tam giác AED vuông tại E.
Mà tam giác ABD = tam giác AED (cmt).
\(\Rightarrow\) Tam giác ABD vuông tại B.
\(\Rightarrow\) \(\widehat{ABD}\) \(=90^o.\)
\(\Rightarrow\) Tam giác ABC vuông tại B.
Vậy để DE \(\perp\) AC thì tam giác ABC vuông tại B.
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
BD=CE
\(\widehat{ABD}=\widehat{ACE}\)
Do đó: ΔABD=ΔACE
Suy ra: AB=AC
hay ΔABC cân tại A
b: XétΔABC có
AD là đường cao
CH là đường cao
AD cắt CH tại D
Do đó: D là trực tâm của ΔABC
=>BD vuông góc với AC
(
Thông cảm mk bị cận!
,tuy mk vẽ hơi xấu nhưng các bn cố gắng giúp mk nha!!!!!!!!!!!!
Kẻ Cz//By (z thuộc nửa mặt phẳng bờ AC chứa B)
Ta có: góc zCB=góc CBy = 30 độ (so le trong)
Mà góc zCB + góc zCA=120 độ
=> góc zCA=90 độ.
=> Cz//Ax (cùng vuông góc AC)
Mà Cz//By => Ax//By
\(\frac{B}{A}=\frac{2^2+4^2+6^2+...+200^2}{1^2+2^2+...+100^2}=\frac{\left(1.2\right)^2+\left(2.2\right)^2+...+\left(100.2\right)^2}{1^2+2^2+...+100^2}\)
\(=\frac{1^2.2^2+2^2.2^2+...+100^2+2^2}{1^2+2^2+...+100^2}\)
\(=\frac{\left(1^2+2^2+...+100^2\right).2^2}{1^2+2^2+100^2}\)
\(=2^2=4\)
Vậy \(\frac{B}{A}=4\)
Sửa lại: ( tại nhìn bé quá, tưởng mũ 3 -> mũ 2 )
\(\frac{B}{A}=\frac{2^3+4^3+6^3+...+200^3}{1^3+2^3+...+100^3}\)
\(\Rightarrow\frac{B}{A}=\frac{\left(1.2\right)^3+\left(2.2\right)^3+...+\left(100.2\right)^3}{1^3+2^3+...+100^3}\)
\(\Rightarrow\frac{B}{A}=\frac{1^3.2^3+2^3.2^3+...+100^3.2^3}{1^3+2^3+...+100^3}\)
\(\Rightarrow\frac{B}{A}=\frac{\left(1^3+2^3+...+100^3\right)2^3}{1^3+2^3+...+100^3}\)
\(\Rightarrow\frac{B}{A}=2^3=8\)
Vậy \(\frac{B}{A}=8\)
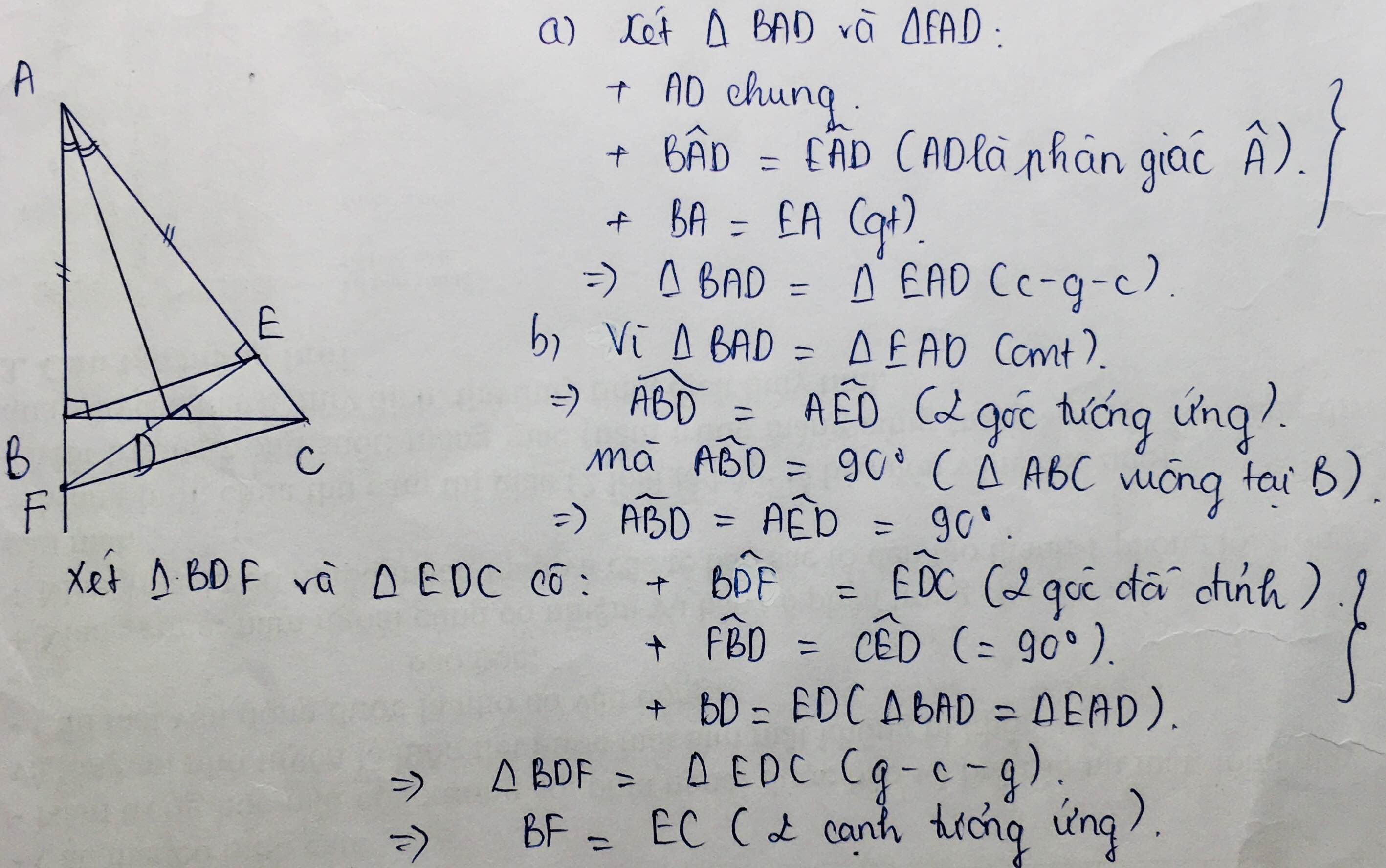
a: Xét tứ giác EFBC có
A là trung điểm của EB
A là trung điểm của CF
Do đó: EFBC là hình bình hành
Suy ra: EF=BC