Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu tâm I(1;-2;3) và đi qua điểm A(-1;2;1) có phương trình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 5 2019
Đáp án A
Xét mặt cầu S : x − 1 2 + y + 3 2 + z 2 = 5 có tâm I 1 ; − 3 ; 0 và bán kính R = 5
CM
7 tháng 5 2018
Đáp án D
d ( I , O y z ) = R = 1 ⇒ x − 1 2 + y + 4 2 + z − 3 2 = 1
CM
30 tháng 3 2019
Đáp án D
d(I,Oyz)=R=1 ⇒ ( x - 1 ) 2 + ( y + 4 ) 2 + ( z - 3 ) 2 = 1
CM
28 tháng 2 2018
Đáp án A
Tọa độ tâm và bán kính của mặt cầu là I(-1;3;0), R=4.
CM
12 tháng 6 2019
Đáp án A.
Mặt phẳng (P) qua I và vuông góc với Oy là:
=> bán kính mặt cầu tâm I và tiếp xúc với trục Oy là:
= 10
=> Phương trình mặt cầu tâm I và tiếp xúc với trục Oy là:
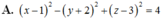
Lời giải:
Bán kính mặt cầu:
$IA=\sqrt{(x_I-x_A)^2+(y_I-y_A)^2+(z_I-z_A)^2}$
$=\sqrt{(1--1)^2+(-2-2)^2+(3-1)^2}=2\sqrt{6}$
PTMC cần tìm:
$(x-x_I)^2+(y-y_I)^2+(z-z_I)^2=IA^2$
$\Leftrightarrow (x-1)^2+(y+2)^2+(z-3)^2=24$