Tìm GTNN của sin6x+cos6x với 0o<x<90o
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
2
6 tháng 9 2021
\(y=\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)+\cos4x-1\)
\(\sin^6x+\cos^6x=\left(\sin^2x+\cos^2x\right)\left(\sin^4x-\sin^2x\cdot\cos^2x+\cos^4x\right)\\ =\left(\sin^2x+\cos^2x\right)^2-3\sin^2x\cdot\cos^2x=1-\dfrac{3}{4}\sin^22x\)
Do \(0\le\sin^22x\le1\Leftrightarrow\dfrac{3}{4}\cdot0\ge-\dfrac{3}{4}\sin^22x\ge-\dfrac{3}{4}\)
\(\Leftrightarrow1\ge1-\dfrac{3}{4}\sin^22x\ge1-\dfrac{3}{4}=\dfrac{1}{4}\\ \Leftrightarrow\dfrac{4}{3}\ge\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)\ge\dfrac{1}{4}\cdot\dfrac{4}{3}=\dfrac{1}{3}\)
Ta có \(-1\le\cos4x\le1\)
\(\Leftrightarrow\dfrac{1}{3}-1-1\le\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)+\cos4x-1\le\dfrac{4}{3}+1-1\\ \Leftrightarrow-\dfrac{5}{3}\le y\le\dfrac{4}{3}\)
Vậy \(y_{min}=-\dfrac{5}{3};y_{max}=\dfrac{4}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 9 2021
\(y=\dfrac{4}{3}\left(sin^6x+cos^6x\right)+cos4x-1\)
\(y=\dfrac{4}{3}\left(\dfrac{5}{8}+\dfrac{3}{8}cos4x\right)+cos4x-1\)
\(y=\dfrac{3}{2}cos4x-\dfrac{1}{6}\)
\(-1\le cos4x\le1\Rightarrow-\dfrac{5}{3}\le y\le\dfrac{4}{3}\)
\(y_{min}=-\dfrac{5}{3}\) khi \(cos4x=-1\)
\(y_{max}=\dfrac{4}{3}\) khi \(cos4x=1\)
PT
1
CM
20 tháng 8 2017
Đáp án B
Ta có y = sin 6 x + cos 6 x + 3 sin 2 x c os 2 x = 1 − 3 4 sin 2 2 x + 3 4 sin 2 2 x = 1 ⇒ y ' = 0.
PT
1
CM
7 tháng 1 2018
Đáp án: C
Ta có:
sin 6 x + c o s 6 x = ( sin 2 x ) 3 + ( cos 2 x ) 3
= ( sin 2 x + c o s 2 x )( sin 4 x - sin 2 x cos 2 x + c o s 4 x )
= sin 4 x - sin 2 x cos 2 x + c o s 4 x
= ( sin 2 x + cos 2 x ) 2 - 3 sin 2 x cos 2 x
= 1 - 3 sin 2 x cos 2 x
= 1 - (3/4) sin 2 2 x
Vì
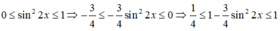
Vậy giá trị nhỏ nhất của sin 6 x + c o s 6 x là 1/4
Dấu “=” xảy ra ⇔ sin 2 2 x = 1 ⇔ sin2x = 1 hoặc sin2x = -1
PT
1
CM
26 tháng 9 2019
Chọn B.
Ta có A = sin6x + cos6x + 3sin2x.cos2x.
= ( sin2x)3 + (cos2x)3 + 3sin2x.cos2x.
= (sin2x + cos2x)3 - 3sin2x.cos2x(sin2x + cos2x) + 3.sin2x.cos2x
= 1 - 3.sin2x.cos2x + 3.sin2x.cos2x = 1
PT
1
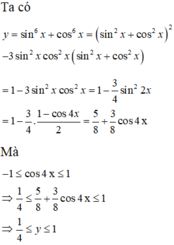
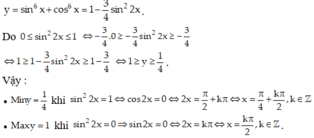
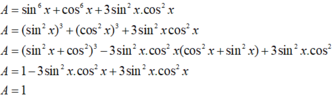
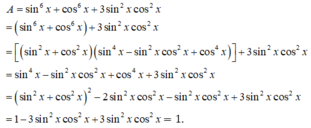
\(sin^6x+cos^6x=\left(sin^2x+cos^2x\right)\left(sin^4x-sin^2xcos^2x+cos^4x\right)\)
\(=sin^4x-cos^2xsin^2x+cos^4x\)\(=\left(sin^2x+cos^2x\right)^2-3sin^2xcos^2x\)
\(=1-3sin^2xcos^2x\).
Như vậy \(sin^6x+cos^6x\) đạt giá trị nhỏ nhất khi \(3sin^2xcos^2x\) đạt GTLN.
Mà \(3sin^2xcos^2x\le3.\left(\frac{sin^2x+cos^2x}{2}\right)^2=\frac{3}{4}\).
Dấu bằng xảy ra khi và chỉ khi: \(sinx=cosx\) hay \(x=45^o\).
vậy GTNN của \(sin^6x+cos^6x=1-\frac{3}{4}=\frac{1}{4}\) khi \(x=45^o\).