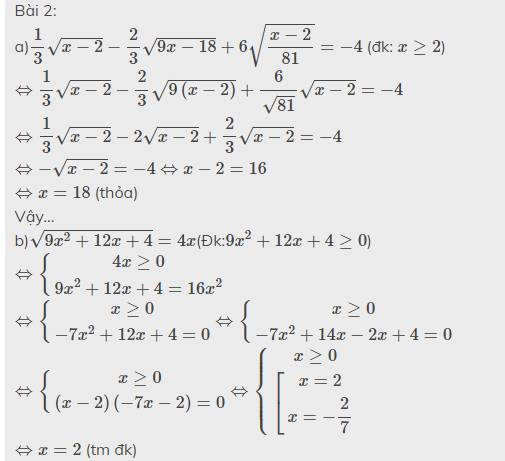\(\sqrt{2}.\left(\sqrt{ }21+3\right)+\sqrt{5-\sqrt{ }21}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)\(\left(\sqrt{21}+7\right)\cdot\sqrt{10-2\sqrt{21}}\)
\(=\left(\sqrt{21}+7\right)\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}\)
\(=\sqrt{7}\left(\sqrt{3}+\sqrt{7}\right)\left(\sqrt{7}-\sqrt{3}\right)\)
\(=\sqrt{7}\left(7-3\right)=4\sqrt{7}\)
b)\(\left(7+\sqrt{14}\right)\sqrt{9-2\sqrt{14}}\)
\(=\left(7+\sqrt{14}\right)\sqrt{\left(\sqrt{7}-\sqrt{2}\right)^2}\)
\(=\sqrt{7}\left(\sqrt{7}+\sqrt{2}\right)\left(\sqrt{7}-\sqrt{2}\right)\)
\(=\sqrt{7}\left(7-2\right)=5\sqrt{7}\)

Bài 1
a) Đặt VT = A
<=> \(2\sqrt{2}A=\left(8+2\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right)\sqrt{8-2\sqrt{15}}\)
<=> \(2\sqrt{2}A=\left(\sqrt{5}+\sqrt{3}\right)^2.\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right).\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\)
<=> \(2A=\left(\sqrt{5}+\sqrt{3}\right)^2.\left(\sqrt{5}-\sqrt{3}\right)^2\)
<=> 2A = \(\left(5-3\right)^2=4\)
<=> A = 2
b) Đặt VT = B
<=> \(2\sqrt{2}B=\left(10+2\sqrt{21}\right).\left(\sqrt{14}-\sqrt{6}\right)\sqrt{10-2\sqrt{21}}\)
<=> \(2\sqrt{2}B=\left(\sqrt{7}+\sqrt{3}\right)^2.\sqrt{2}\left(\sqrt{7}-\sqrt{3}\right).\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}\)
<=> \(2B=\left(\sqrt{7}+\sqrt{3}\right)^2.\left(\sqrt{7}-\sqrt{3}\right)^2=\left(7-3\right)^2=16\)
<=> B = 8
Bài 2
Đặt VT = A
<=> A2 = \(\dfrac{\sqrt{5}+2+\sqrt{5}-2+2\sqrt{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}}{2}\)
<=> A2 = \(\dfrac{2\sqrt{5}+2\sqrt{5-4}}{2}=\dfrac{2\sqrt{5}+2}{2}=\sqrt{5}+1\)
<=> \(A=\sqrt{\sqrt{5}+1}\)

`a)A=(3-sqrt5)sqrt{3+sqrt5}+(3+sqrt5)sqrt{3-sqrt5}`
`=sqrt{3-sqrt5}sqrt{3+sqrt5}(sqrt{3+sqrt5}+sqrt{3-sqrt5})`
`=sqrt{9-5}(sqrt{3+sqrt5}+sqrt{3-sqrt5})`
`=2(sqrt{3+sqrt5}+sqrt{3-sqrt5})`
`=sqrt2(sqrt{6+2sqrt5}+sqrt{6-2sqrt5})`
`=sqrt2(sqrt{(sqrt5+1)^2}+sqrt{(sqrt5+1)^2})`
`=sqrt2(sqrt5+1+sqrt5-1)`
`=sqrt{2}.2sqrt5`
`=2sqrt{10}`
`b)B=(5+sqrt{21})(sqrt{14}-sqrt6)sqrt{5-sqrt{21}}`
`=sqrt{5+sqrt{21}}sqrt{5-sqrt{21}}sqrt{5+sqrt{21}}(sqrt{14}-sqrt6)`
`=sqrt{25-21}sqrt{5+sqrt{21}}(sqrt{14}-sqrt6)`
`=2sqrt{5+sqrt{21}}(sqrt{14}-sqrt6)`
`=2sqrt2sqrt{5+sqrt{21}}(sqrt{7}-sqrt3)`
`=2sqrt{10+2sqrt{21}}(sqrt{7}-sqrt3)`
`=2sqrt{(sqrt3+sqrt7)^2}(sqrt{7}-sqrt3)`
`=2(sqrt3+sqrt7)(sqrt{7}-sqrt3)`
`=2(7-3)`
`=8`
`c)C=sqrt{4+sqrt7}-sqrt{4-sqrt7}`
`=sqrt{(8+2sqrt7)/2}-sqrt{(8-2sqrt7)/2}`
`=sqrt{(sqrt7+1)^2/2}-sqrt{(sqrt7+1)^2/2}`
`=(sqrt7+1)/sqrt2-(sqrt7-1)/2`
`=2/sqrt2=sqrt2`

b: \(=\left(5+\sqrt{21}\right)\left(\sqrt{7}-\sqrt{3}\right)\sqrt{10-2\sqrt{21}}\)
\(=\left(5+\sqrt{21}\right)\left(10-2\sqrt{21}\right)\)
\(=50-10\sqrt{21}+10\sqrt{21}-42=8\)
a: \(A=\sqrt{\sqrt{2}-1}+\sqrt{\sqrt{2}+1}\)
=>\(A^2=\sqrt{2}-1+\sqrt{2}+1+2\sqrt{2-1}=2\sqrt{2}+2\)
=>\(A=\sqrt{2\sqrt{2}+2}\)
Đặt \(B=\sqrt{\sqrt{2}-1}+\sqrt{\sqrt{2}+1}-\sqrt{2+\sqrt{2}}\)
=>\(B=\sqrt{2\sqrt{2}+2}-\sqrt{2+\sqrt{2}}\)
=>\(B^2=2\sqrt{2}+2+2+\sqrt{2}-2\sqrt{\sqrt{2}\left(2+\sqrt{2}\right)\left(2+\sqrt{2}\right)}\)
=>\(B^2=4+3\sqrt{2}-2\sqrt[4]{2}\left(2+\sqrt{2}\right)\)
=>\(B\simeq0,35\)

Bài 2:
a)\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\) (đk: \(x\ge2\))
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9\left(x-2\right)}+\dfrac{6}{\sqrt{81}}\sqrt{x-2}=-4\)
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-2\sqrt{x-2}+\dfrac{2}{3}\sqrt{x-2}=-4\)
\(\Leftrightarrow-\sqrt{x-2}=-4\) \(\Leftrightarrow x-2=16\)
\(\Leftrightarrow x=18\) (thỏa)
Vậy...
b)\(\sqrt{9x^2+12x+4}=4x\)(Đk:\(9x^2+12x+4\ge0\))
\(\Leftrightarrow\left\{{}\begin{matrix}4x\ge0\\9x^2+12x+4=16x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+12x+4=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+14x-2x+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(x-2\right)\left(-7x-2\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x=2\\x=-\dfrac{2}{7}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x=2\) (tm đk)
Vậy...
c) \(\sqrt{x-2\sqrt{x-1}}=\sqrt{x-1}\) (đk: \(x\ge1\))
\(\Leftrightarrow x-2\sqrt{x-1}=x-1\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{1}{2}\) \(\Leftrightarrow x=\dfrac{5}{4}\) (tm)
Vậy...