Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là tâm của chiếc đĩa
\( \Rightarrow \) OA = OB = OC = r ( do cùng có độ dài = bán kính )
Xét tam giác ABC có O là điểm cách đều A, B, C
\( \Rightarrow \) O là giao của 3 đường trung trực tam giác ABC
Để xác định O ta vẽ 2 đường trung trực của AB, BC chúng cắt nhau tại O .

Đáp án A
Ta có thể nhận thấy đường sinh của hình nón là bán kính của đĩa tròn. Còn chu vi đáy của hình nón chính là chu vi của đĩa trừ đi độ dài cung tròn đã cắt. Như vậy ta tiến hành giải chi tiết như sau:


* Chứng minh
Lần cân thứ nhất: mT = mb + mn + mv + m1 (1).
Lần cân thứ hai: mT = mb + (mn – mn0) + mv + m2 (2).
Trong phương trình (1), mn là khối lượng của nước chứa trong bình tới vạch đánh dấu, mb là khối lượng vỏ bình, mv là khối lượng vật.
Trong phương trình (2), mn0 là khối lượng của phần nước bị vật chiếm chỗ.
Vì mT là không thay đổi nên từ (1), (2) ta có:
mb + mn + mv + m1 = mb + (mn – mn0) + mv + m2
↔ mn0 = m2 – m1.
Vì 1 gam nước nguyên chất có thể tích là 1cm3, nên số đo khối lượng mn theo đơn vị gam là số đo có thể tích của phần nước bị vật chiếm chỗ theo đơn vị cm3.
Thể tích của phần nước bị vật chiếm chỗ chính là thể tích của vật. Do đó thể tích của vật tính ra cm3 có độ lớn bằng V = m2 – m1.
* Cách xác định vật thể như trên chính xác hơn cách xác định bằng bình chia độ, đo khối lượng bằng cân Rôbécvan chính xác hơn đo thể tích bằng bình chia độ do:
+ GHĐ của cân Rôbécvan nhỏ hơn GHĐ của bình chia độ rất nhiều.
+ Cách đọc mực nước ở bình chia độ khó chính xác hơn cách theo dõi kim của cân ở vị trí cân bằng. Mặt khác, cách cân hai lần như trên loại trừ được những sai số do cân cấu tạo không được tốt, chẳng hạn hai phần của đòn cân không thật bằng nhau về chiều dài cũng như khối lượng.

Gọi phần cung tròn bị cắt có góc ở tâm bằng x độ \(\left(0< x< 360\right)\)
Chu vi đường tròn ban đầu: \(2\pi R\)
Chu vi sau khi bị cắt: \(2\pi R\left(1-\dfrac{x}{360}\right)\)
(Và lưu ý chu vi này đúng bằng chu vi đường tròn đáy hình nón được tạo ra, đường sinh nón bằng R)
Gọi đáy nón có bán kính \(r\)
\(\Rightarrow2\pi r=2\pi R\left(1-\dfrac{x}{360}\right)\Rightarrow r=R\left(1-\dfrac{x}{360}\right)\)
\(\Rightarrow V_{nón}=\dfrac{1}{3}\pi r^2.\sqrt{R^2-r^2}=f\left(x\right)\)
Giờ chắc khảo sát hàm \(f\left(x\right)\) tìm x là được

Chọn đáp án D
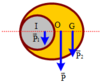
Do tính đối xúng → G nằm trên đường thẳng OO' về phía đầy
Trọng tâm của đĩa nguyên vẹn là tâm O; trọng tâm của đĩa bị khoét là O'


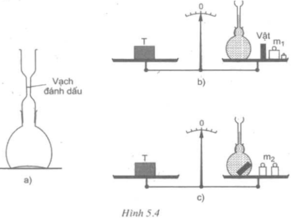
Lần cân thứ nhất: mT = mb + mn + mv + m1 (1).
Lần cân thứ hai: mT = mb + (mn – mn0) + mv + m2 (2).
Trong phương trình (1), mn là khối lượng của nước chứa trong bình tới vạch đánh dấu, mb là khối lượng vỏ bình, mv là khối lượng vật.
Trong phương trình (2), mn0 là khối lượng của phần nước bị vật chiếm chỗ.
Vì mT là không thay đổi nên từ (1), (2) ta có:
mb + mn + mv + m1 = mb + (mn – mn0) + mv + m2
↔ mn0 = m2 – m1.
Vì 1 gam nước nguyên chất có thể tích là 1cm3, nên số đo khối lượng mn theo đơn vị gam là số đo có thể tích của phần nước bị vật chiếm chỗ theo đơn vị cm3.
Thể tích của phần nước bị vật chiếm chỗ chính là thể tích của vật. Do đó thể tích của vật tính ra cm3 có độ lớn bằng V = m2 – m1.
* Cách xác định vật thể như trên chính xác hơn cách xác định bằng bình chia độ, đo khối lượng bằng cân Rôbécvan chính xác hơn đo thể tích bằng bình chia độ do:
+ GHĐ của cân Rôbécvan nhỏ hơn GHĐ của bình chia độ rất nhiều.
+ Cách đọc mực nước ở bình chia độ khó chính xác hơn cách theo dõi kim của cân ở vị trí cân bằng. Mặt khác, cách cân hai lần như trên loại trừ được những sai số do cân cấu tạo không được tốt, chẳng hạn hai phần của đòn cân không thật bằng nhau về chiều dài cũng như khối lượng.

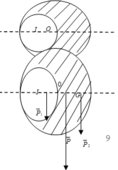
Do tính đối xứng G nằm trên đường thẳng OO’ về phía đầy.
Trọng tâm của đĩa nguyên vẹn là tâm O; trọng tâm của đĩa bị khoét là O’.
P → là hợp lực của hai lực P → 1 , P → 2 .
O G O O ' = P 2 P 1 = m 2 m 1 = V 2 V 1 = S 2 S 1 = π R 2 4 3 π R 2 4 = 1 3 ⇒ O G = R 6


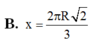
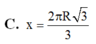
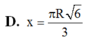

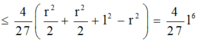
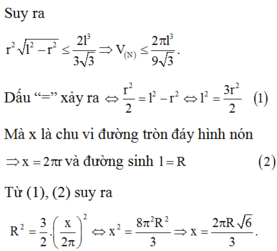
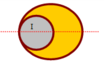
Lấy ba điểm A, B, C trên phần còn lại của cái đĩa tạo thành tam giác
Vẽ hai đường trung trực của tam giác tạo thành từ ba điểm đó
Giao điểm O của hai đường trung trực là tâm của cái đĩa
Bán kính cái đĩa cần tìm là OA.