Giả sử phương trình x² - (2m + 1)x + m² 1 = 0 (m là tham số) có hai nghiệm phân biệt x1, x2 giá trị lớn nhất của biểu thức A = (2x1 - x2) x (x1 - 2x2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 10 2019
a. + Với m = − 1 2 phương trình (1) trở thành x 2 − 4 x = 0 ⇔ x = 0 x = 4 .
+ Vậy khi m = − 1 2 phương trình có hai nghiệm x= 0 và x= 4.
b. + Phương trình có hai nghiệm dương phân biệt khi
Δ = 2 m + 5 2 − 4 2 m + 1 > 0 x 1 + x 2 = 2 m + 5 > 0 x 1 . x 2 = 2 m + 1 > 0
+ Ta có Δ = 2 m + 5 2 − 4 2 m + 1 = 4 m 2 + 12 m + 21 = 2 m + 3 2 + 12 > 0 , ∀ m ∈ R
+ Giải được điều kiện m > − 1 2 (*).
+ Do P>0 nên P đạt nhỏ nhất khi P 2 nhỏ nhất.
+ Ta có P 2 = x 1 + x 2 − 2 x 1 x 2 = 2 m + 5 − 2 2 m + 1 = 2 m + 1 − 1 2 + 3 ≥ 3 ( ∀ m > − 1 2 ) ⇒ P ≥ 3 ( ∀ m > − 1 2 ) .
và P = 3 khi m= 0 (thoả mãn (*)).
+ Vậy giá trị nhỏ nhất P = 3 khi m= 0.
2 tháng 7 2023
a: Δ=(2m-1)^2-4*(-1)(m-m^2)
=4m^2-4m+1+4m-4m^2=1>0
=>(1) luôn có hai nghiệm phân biệt
b: m=x1-2x1x2+x2-2x1x2
=x1+x2-4x1x2
=2m-1+4(m-m^2)
=>m-2m+1-4m+4m^2=0
=>4m^2-5m+1=0
=>m=1 hoặc m=1/4
c: x1+x2-2x1x2
=2m-1+2m-2m^2=-2m^2+4m-1
=-2m^2+4m-2+1
=-2(m-1)^2+1<=1
CM
21 tháng 10 2019
Phương trình 2 x 2 - 4 m x - 1 = 0 có ∆ ' = 4 m 2 + 2 > 0 nên phương trình có hai nghiệm phân biệt x 1 , x 2 với S = x 1 + x 2 = 2 m , P = x 1 x 2 = - 1 2
Ta có: T 2 = x 1 - x 2 2 = S 2 - 4 P = 4 m 2 + 2 ≥ 2 ⇒ T ≥ 2
Dấu bằng xảy ra khi m = 0.
Vậy m i n T = 2
Đáp án cần chọn là: B
CM
25 tháng 12 2017
Chọn đáp án C
Phương pháp
+) Đặt điều kiện để phương trình có nghĩa.
+) Đặt ẩn phụ để giải phương trình: log 2 x = t . Tìm điều kiện để phương trình có nghiệm.
+) Dựa vào dữ kiện x 1 + x 2 = 6 tìm m. Từ đó tính x 1 - x 2 .
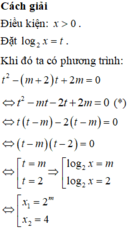
Phương trình đã cho có hai nghiệm phân biệt: x 1 , x 2 ⇔ phương trình (*) có hai nghiệm phân biệt ⇔ m ≠ 2 .
16 tháng 2 2023
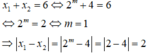
Δ=(-2)^2-4(m-1)
=-4m+4+4
=-4m+8
Để phương trình có hai nghiệm phân biệt thì -4m+8>0
=>-4m>-8
=>m<2
x1^2+x2^2-3x1x2=2m^2+|m-3|
=>2m^2+|m-3|=(x1+x2)^2-5x1x2=2^2-5(m-1)=4-5m+5=-5m+9
TH1: m>=3
=>2m^2+m-3+5m-9=0
=>2m^2+6m-12=0
=>m^2+3m-6=0
=>\(m\in\varnothing\)
TH2: m<3
=>2m^2+3-m+5m-9=0
=>2m^2+4m-6=0
=>m^2+2m-3=0
=>(m+3)(m-1)=0
=>m=1 hoặc m=-3
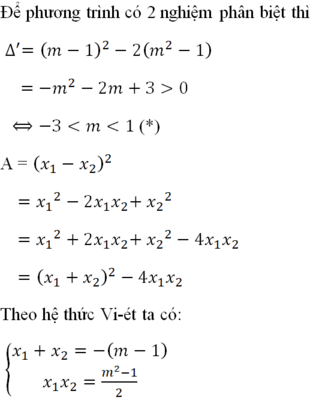
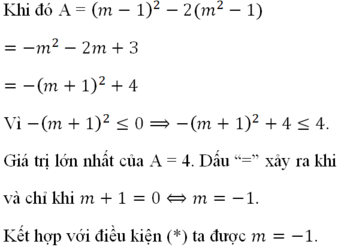
\(x^2-\left(2m+1\right)x+m^2+1=0\)
\(\text{Δ}=\left(2m+1\right)^2-4\cdot1\cdot\left(m^2+1\right)\)
\(=4m^2+4m+1-4m^2-4=4m-3\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>4m-3>0
=>4m>3
=>\(m>\dfrac{3}{4}\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+1\\x_1x_2=\dfrac{c}{a}=m^2+1\end{matrix}\right.\)
\(A=\left(2x_1-x_2\right)\left(x_1-2x_2\right)\)
\(=2x_1^2+2x_2^2-5x_1x_2\)
\(=2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]-5x_1x_2\)
\(=2\left[\left(2m+1\right)^2-2\left(m^2+1\right)\right]-5\left(m^2+1\right)\)
\(=2\left(2m+1\right)^2-9\left(m^2+1\right)\)
\(=2\left(4m^2+4m+1\right)-9m^2-9\)
\(=8m^2+8m+2-9m^2-9\)
\(=-m^2+8m-7\)
\(=-\left(m^2-8m+7\right)\)
\(=-\left(m^2-8m+16-9\right)\)
\(=-\left(m-4\right)^2+9< =9\forall m\)
Dấu '=' xảy ra khi m=4