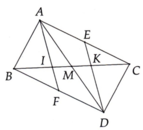
Cho tam giác ABC . Lấy M là điểm bất kỳ trên BC. Vẽ I là trung điểm của AM.
Từ J kẻ IK //AB (K thuộc AB)
a)tính tỉ số IK/AB
b) Tia BI cắt AC tại N, tia CI cắt AB tại E. Chứng minh BI/BN+CI/CE=3/2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

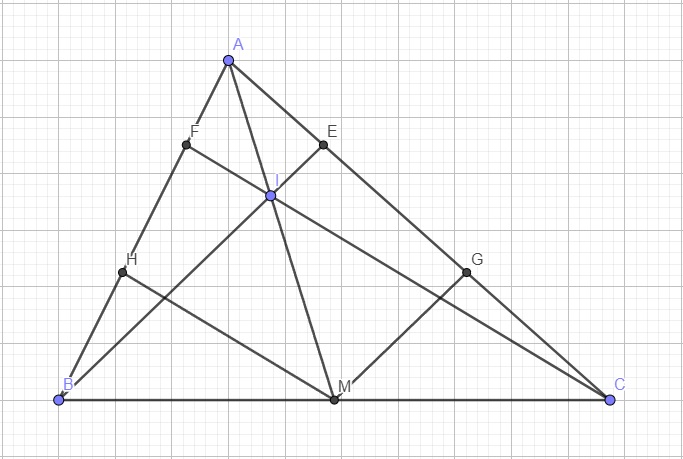
Qua M kẻ các đường thẳng song song BE và CF lần lượt cắt AC và AB tại G và H
Do M là trung điểm BC và \(MG||BE\Rightarrow MG\) là đường trung bình tam giác BCE
\(\Rightarrow G\) là trung điểm CE \(\Rightarrow GE=GC=\dfrac{1}{2}EC\)
Tương tự ta có H là trung điểm BF \(\Rightarrow BH=FH=\dfrac{1}{2}BF\)
Áp dụng định lý Talet trong tam giác AMG:
\(\dfrac{AE}{EG}=\dfrac{AI}{IM}\)
Áp dụng định lý Talet trong tam giác AMH:
\(\dfrac{AF}{FH}=\dfrac{AI}{IM}\)
\(\Rightarrow\dfrac{AE}{EG}=\dfrac{AF}{FH}\Rightarrow\dfrac{AE}{2EG}=\dfrac{AF}{2FH}\Rightarrow\dfrac{AE}{EC}=\dfrac{AF}{FB}\)
\(\Rightarrow EF||BC\) (định lý talet đảo)

a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét tứ giác ANMC có
I là trung điểm của AM
I là trung điểm của CN
Do đó: ANMC là hình bình hành
Suy ra: AN//MC
hay AN//BC
c: Xét tứ giác ABMK có
I là trung điểm của BK
I là trung điểm của AM
Do đó: ABMK là hình bình hành
Suy ra: AK//BM
hay AK//BC
mà AN//BC
và AN,AK có điểm chung là A
nên A,N,K thẳng hàng

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét tứ giác ANMC có
I là trung điểm của AM
I là trung điểm của NC
Do đó: ANMC là hình bình hành
Suy ra: AN//MC
hay AN//BC


giúp mk với
Cho tam giác ABC lấy m là điểm bất kì trên BC vẽ I là trung điểm của am từ y kẻ ik song song với AB k không thuộc BC tính tỉ số ik phần AB