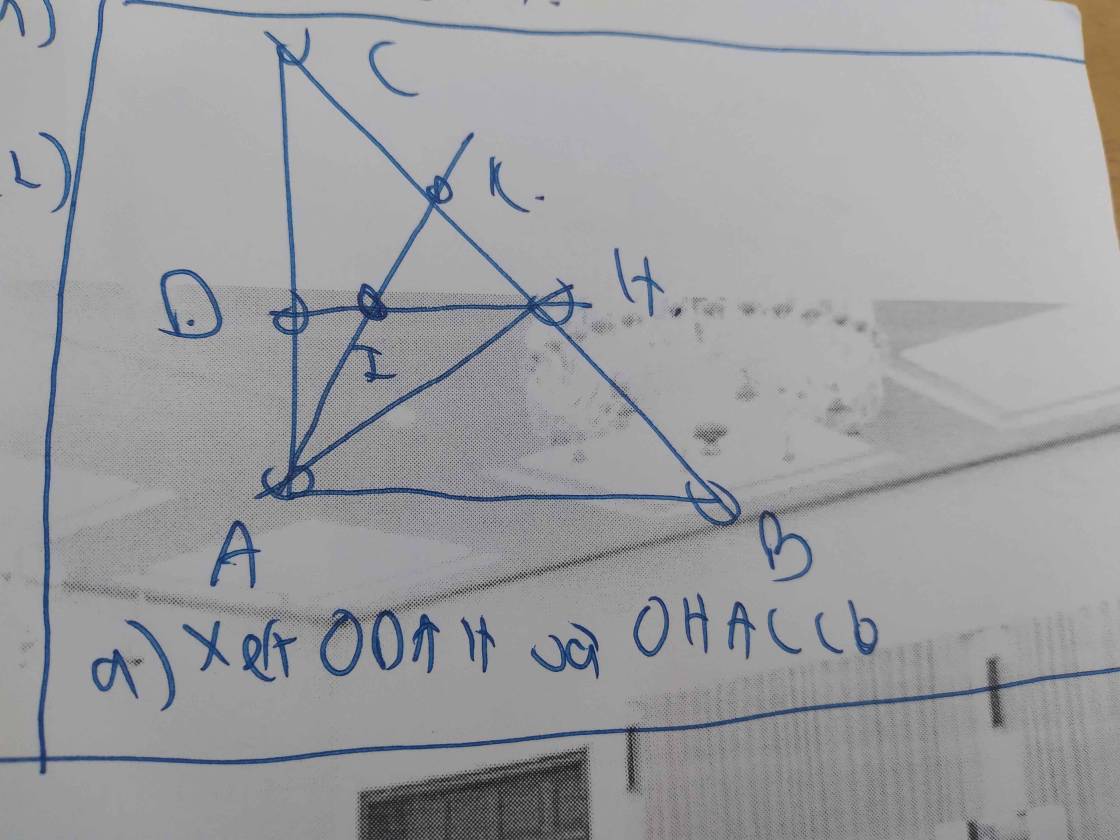
Cho tam giác ABC vuông tại A có đường cao AH (H ∈ BC), kẻ HD vuông góc với AC tại D (D ∈ AC). a) Chứng minh: ∆DAH đồng dạng với ∆HAC từ đó suy ra AH^2 = AD. AC b) Từ A vẽ đường phân giác của góc HAC cắt HD, BC lần lượt tại I và K. Chứng minh: AH. AI = AD. AK và ∆HIK cân. c) Từ C vẽ CJ vuông góc với AK (J ∈ AK). Chứng minh: AK^2 = AH. AC − HK. KC
Vẽ Hình cho mình nữa với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔDAH vuông tại D và ΔHAC vuông tại H có
\(\widehat{DAH}\) chung
Do đó: ΔDAH\(\sim\)ΔHAC(g-g)

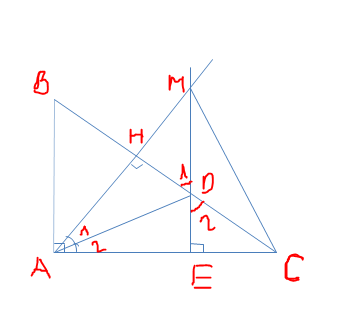
a/ Xét \(\Delta\) vuông AHD và \(\Delta\) AED. Có:
\(\widehat{A1}\)= \(\widehat{A2}\) ( giả thiết)
AD chung
=> \(\Delta AHD=\Delta AED\) ( ch-gn)
=> DH = DE ( 2 cạnh tương ứng )
b/ BMC không cân được bạn nhé. bạn chép nhầm đề bài r: Chứng minh DMC cân mới đúng.
Xét \(\Delta vuôngHDM\) và \(\Delta vuôngEDC\). Có:
\(\widehat{D1}\) = \(\widehat{D2}\) ( đối đỉnh)
HD = HE ( cmt)
=> \(\Delta HDM=\Delta EDC\left(cgv-gnk\right)\)
=> DM = DC ( 2 cạnh tương ứng)
=> Xét \(\Delta DMCcóDM=DC=>\Delta DMCcân\left(cântạiD\right)\)
~ Cậu ktra lại nhé~

a) ta có
goc BAD+ goc DAC =90 (2 góc kề phụ)
goc ADB+goc HAD=90 ( tam giác AHD vuông tại H)
goc DAC=goc HAD (AD lả p/g goc HAC)
==> góc BAD= goc ADB
-> tam giac BAD cân tại B
b) xet tam giac ADH và tam giac ADE ta có
AD= AD ( cạnh chung)
goc HAD = goc DAC ( AD là p/g goc HAC)
goc AID = góc AIE (=90)
--> tam giac ADH= tam giac ADE (g-c-g)
-< AH= AE ( 2 canh tương ứng)
Xét tam giac AHD và tam giac AED ta có
AD=AD ( cạnh chung)
AH=AE (cmt)
goc DAH= goc DAE ( AD là p/g HAC)
-> tam giac AHD= tam giac AED ( c-g-c)
-> goc AHD= goc AED ( 2 góc tương ứng
mà góc AHD = 90 ( AH vuông góc BC)
nên AED =90
-> DE vuông góc AC
c) Xét tam giac ABH vuông tại H ta có
AB2= AH2+BH2 ( dly pi ta go)
152=122+BH2
BH2 =152-122=81
BH=9
ta có BA=BD ( tam giác ABD cân tại B)
BA=15 cm (gt)
-> BD=15
mà BH+HD=BD ( H thuộc BD)
nên 9+HD=15
HD=15-9=6
Xét tam giác ADH vuông tại H ta có
AD2=AH2+HD2 ( định lý pitago)
AD2=122+62=180
-> AD=\(\sqrt{180}=6\sqrt{5}\)
a) Vì BD = BA nên ΔΔBAD cân tại B
=> BADˆBAD^góc BAD = g BDA (góc đáy) →→-> đpcm
b) Ta có: góc BAD + g DAC = 90o
=> g DAC = 90o - g BAD (1)
Áp dụng tc tam giác vuông ta có:
g HAD + g BDA = 90o
=> g HAD = 90o - g BDA (2)
mà góc BAD = g BDA (câu a)
=> gDAC = g HAD
=> AD là tia pg của g HAC.
c) Áp dụng tc tổng 3 góc trong 1 tg ta có:
g AHD + g HDA + g HAD = 180o
=> 90o + g HDA + g HAD = 180o
=> g HDA + g HAD = 90o (3)
g DAC + g DKA + g ADK = 180o
=> g DAC + 90o + g ADK = 180o
=> g DAC + g ADK = 90o (4)
mà gDAC = g HAD hay gDAK = gHAD
Xét tgHAD và tgKAD có:
g HDA = g ADK (c/m trên)
AD chung
g HAD = g DAK (c/m trên)
=> tgHAD = tgKAD (g.c.g)
=> AH = AK (2 cạnh t/ư)