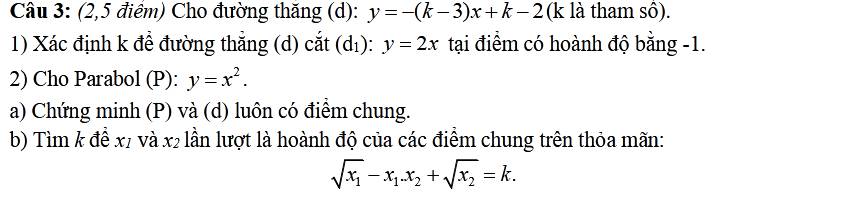
giúp em bài này với ạ , em cần gấp , em cảm ơn nhiều ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HK
1
LW
giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
1
9 tháng 9 2023
3.15:
EF vuông góc MH
NP vuông góc MH
Do đó: EF//NP
3.17:
góc yKH+góc H=180 độ
mà hai góc này là hai góc ở vị trí trong cùng phía
nên Ky//Hx
KA
1
12 tháng 8 2021
nSO3=8/80=0,1(mol)
pthh: SO3 + H2O -> H2SO4
nH2SO4=nSO3=0,1(mol) => mH2SO4(tạo sau)= 0,1.98=9,8(g)
mH2SO4(tổng)= 100.9,8% + 9,8=19,6(g)
mddH2SO4(sau)=8+100=108(g)
=>C%ddH2SO4(sau)= (19,6/108).100=18,148%
V
0
TD
2
Q
19 tháng 5 2021
vẽ lại mạch ta có RAM//RMN//RNB
đặt theo thứ tự 3 R là a,b,c
ta có a+b+c=1 (1)
điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0
áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)
\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)
dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)
từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)
vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )
LW
2
AH
Akai Haruma
Giáo viên
9 tháng 9 2023
3.14:
Ta thấy $\widehat{xNM}=\widehat{xQP}=45^0$. Mà 2 góc này ở vị trí đồng vị nên $MN\parallel PQ$
3.15
$EF\parallel NP$ do cùng vuông góc với $MH$
AH
Akai Haruma
Giáo viên
9 tháng 9 2023
3.16: Bạn tự vẽ hình nhé.
3.17:
Ta thấy $\widehat{yKH}+\widehat{KHx}=130^0+50^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $Ky\parallel Hx$
HK
1
HK
1
10 tháng 7 2023
a: Khi x=2 thì (1) sẽ là:
4-2(m+2)+m+1=0
=>m+5-2m-4=0
=>1-m=0
=>m=1
x1+x2=m+1=3
=>x2=3-2=1
b: Δ=(m+2)^2-4(m+1)
=m^2+4m+4-4m-4=m^2>=0
=>Phương trình luôn có hai nghiệm
P=(x1+x2)^2-4x1x1+3x1x2
=(x1+x2)^2-x1x2
=(m+2)^2-m-1
=m^2+4m+4-m-1
=m^2+3m+3
=(m+3/2)^2+3/4>=3/4
Dấu = xảy ra khi m=-3/2
15 tháng 11 2021
\(a,=x^2+x+4x+4=\left(x+1\right)\left(x+4\right)\\ b,=x^2+2x-3x-6=\left(x-3\right)\left(x+2\right)\\ c,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ d,=3\left(x^2-2x+5x-10\right)=3\left(x-2\right)\left(x+5\right)\\ e,=-3x^2+6x-x+2=\left(x-2\right)\left(1-3x\right)\\ f,=x^2-x-6x+6=\left(x-1\right)\left(x-6\right)\\ h,=4\left(x^2-3x-6x+18\right)=4\left(x-3\right)\left(x-6\right)\\ i,=3\left(3x^2-3x-8x+5\right)=3\left(x-1\right)\left(3x-8\right)\\ k,=-\left(2x^2+x+4x+2\right)=-\left(2x+1\right)\left(x+2\right)\\ l,=x^2-2xy-5xy+10y^2=\left(x-2y\right)\left(x-5y\right)\\ m,=x^2-xy-2xy+2y^2=\left(x-y\right)\left(x-2y\right)\\ n,=x^2+xy-3xy-3y^2=\left(x+y\right)\left(x-3y\right)\)
1:
Để (d) cắt (d1) thì \(-\left(k-3\right)\ne2\)
=>\(k-3\ne-2\)
=>\(k\ne1\)
Thay x=-1 vào (d1), ta được:
\(y=2\cdot\left(-1\right)=-2\)
Thay x=-1 và y=-2 vào (d), ta được:
\(-\left(k-3\right)\cdot\left(-1\right)+k-2=-2\)
=>\(k-3+k-2=-2\)
=>2k-5=-2
=>2k=3
=>k=1,5(nhận)
2:
a: Phương trình hoành độ giao điểm là:
\(x^2=-\left(k-3\right)x+k-2\)
=>\(x^2+\left(k-3\right)x-k+2=0\)
\(\text{Δ}=\left(k-3\right)^2-4\cdot1\left(-k+2\right)\)
\(=k^2-6k+9+4k-8=k^2-2k+1=\left(k-1\right)^2\)>=0 với mọi k
=>(P) luôn cắt (d)
b:
ĐKXĐ: k<=2
Theo vi-et, ta có:
\(x_1+x_2=-\dfrac{b}{a}=-k+3;x_1x_2=\dfrac{c}{a}=-k+2\)
\(\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=x_1+x_2+2\sqrt{x_1x_2}\)
\(=-k+3+2\sqrt{-k+2}\)
\(=\left(-k+2\right)+2\sqrt{-k+2}+1=\left(\sqrt{-k+2}+1\right)^2\)
=>\(\sqrt{x_1}+\sqrt{x_2}=\sqrt{-k+2}+1\)
\(\sqrt{x_1}+\sqrt{x_2}-x_1x_2=k\)
=>\(\sqrt{-k+2}+1-\left(-k+2\right)=k\)
=>\(\sqrt{-k+2}+1+k-2-k=0\)
=>\(\sqrt{-k+2}-1=0\)
=>-k+2=1
=>-k=-1
=>k=1(nhận)