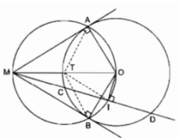
Cho đường tròn (O) và điểm M ở ngoài đường tròn, kẻ hai tiếp tuyến MA, MB,với đường tròn (O) (A, B là các tiếp điểm). Qua M vẽ cát tuyến MCD (MC < MD). Vẽ đường kính EC của đường tròn (O) . Đường thẳng EA cắt đường thẳng BC tại S
a) Chứng minh tứ giác MAOB nội tiếp và SC.SB = SA.SE
b) Chứng minh tam giác ACS đồng dạng tam giác AOM và tam giác MAS cân.
c) Gọi N là giao điểm của hai đường thẳng MO và AE. Chứng minh: góc CBA = góc NDE





a) Ta có ∠MAB + ∠MOB = 90° + 90° = 180° (vì MA, MB là tiếp tuyến của (O) tại A, B)
Suy ra, tứ giác MAOB nội tiếp.
- SC.SB = SA.SE:
Ta có ∠SCE = ∠SAE = 90° (vì EC là đường kính của (O))
Suy ra, tam giác SCE và tam giác SAE vuông cùng tại E và có cạnh chung là SE
Do đó, SC.SB = SA.SE theo định lý hình chiếu.
b) Ta có ∠ACS = ∠AOM = 90° và ∠CAS = ∠MAO (vì tứ giác MAOB nội tiếp)
Suy ra, tam giác ACS đồng dạng tam giác AOM theo định lý đồng dạng tam giác góc-góc.
Ta có ∠MAS = ∠ACS = 90° và ∠AMO = ∠CAO (vì tứ giác MAOB nội tiếp)
Suy ra, tam giác MAS đồng dạng tam giác AOC theo định lý đồng dạng tam giác góc-góc.
Vì vậy, tam giác MAS cân tại A.
c) Ta có ∠CBA = ∠COA (vì tứ giác MAOB nội tiếp)
Và ∠COA = ∠DOE (vì EC là đường kính của (O))
Và ∠DOE = ∠NDE (vì DE // ON)
Suy ra, ∠CBA = ∠NDE.