cho tam giác abc có b=30 độ kẻ ah vuông góc vs bc.Trên tia đối của tia ha lấy e sao cho he=ha a) cm tam giác ahc=ehc.b)cm be vuông góc vs c)tam giác abe là tam giác gì vì sao
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


#\(N\)
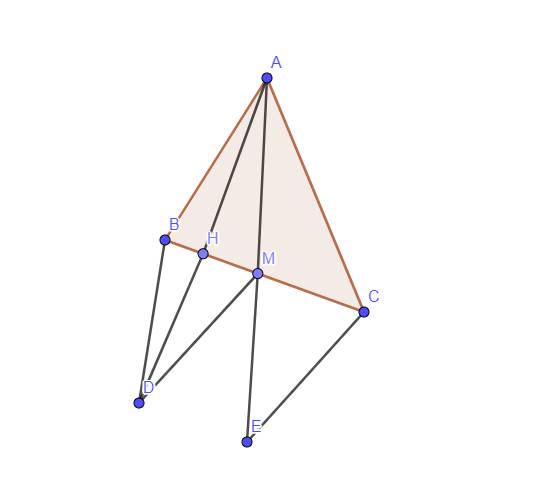
`a,` Xét Tam giác `AMB` và Tam giác `CME` có:
`AM = ME (g``t)`
\(\widehat{AMB}=\widehat{CME}\) `(2` góc đối đỉnh `)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `CME (c-g-c)`
`b,` Vì Tam giác `AMB =` Tam giác `CME (a)`
`-> AB = CE (2` cạnh tương ứng `)`
Xét Tam giác `ABH` và Tam giác `DBH` có:
`HA = HD (g``t)`
\(\widehat{BHA}=\widehat{BHD}=90^0\)
`BH` chung
`=>` Tam giác `ABH =` Tam giác `DBH (c-g-c)`
`=> AB = BD (2` cạnh tương ứng `)`
Mà `AB = CE -> BD = CE`
`c,` Xét Tam giác `AMH` và Tam giác `DMH` có:
`HA = HD (g``t)`
\(\widehat{AHM}=\widehat{DHM}=90^0\)
`HM` chung
`=>` Tam giác `AMH =` Tam giác `DMH (c-g-c)`
`=> AM = DM (2` cạnh tương ứng `)`
Xét Tam giác `AMD` có: `AM = DM`
`->` Tam giác `AMD` là tam giác cân.

a) Xét \(\Delta AHB\)và \(\Delta DHB\)có:
\(AH=DH\left(gt\right)\)
BH là cạnh chung
\(\widehat{AHB}=\widehat{DHB}\left(=90^0\right)\)
\(\Rightarrow\Delta ABH=\Delta DBH\left(c.g.c\right)\)
b) Vì \(\Delta ABH=\Delta DBH\left(cmt\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{DBH}\)( 2 góc tương ứng )
=> BC là tia phân giác \(\widehat{ABD}\)( đpcm )
A)Xét t/giác AHB và t/giác DHB có
AH=AD(gt)
Góc AHB=góc DHB=900
BH là cạnh chung
Suy ra t/giác AHB=t/giác DHB(c-g-c)
B)Ta có Góc ABH=góc DBH( t/giác ABH=t/giác DBH)
Suy ra :BC là tia phân giác của góc ABD
C)Xét t/giác AHM vuông tại H và t/giác FNM vuông tại N
AM=FM(gt)
Góc AHM= góc FMN(2 góc đối đỉnh)
Suy ra t/giác AHM =t/giác FNM( cạnh huyền -góc nhọn)
Suy ra AH=NF (2 cạnh tương ứng)
Mà AH=HD (gt)
Suy ra NF=HD
Chúc bn hc tốt

a,xét tam giác ACH và tam giác DCH có:
HA=HD(gt)
góc CHA= góc CHD(vì CH\(\perp\)AD)
HC chung => tam giác ACH=tam giác DCH(c.g.c)
tam giác ADC có CH vừa là trung tuyến đồng thời là đường cao=>tam giác ADC cân tại C
b,xét tam giác AHB và tam giác DHE có:
góc BHA= góc DHE( đối đỉnh)
HA=HD(cmt), HB=HE(gT)=>tam giác AHB= tam giác DHE(c.g.c)
gọi giao điểm DE với AC là K
vì tam giác AHB= tam giác DHE(cmt)=>góc HED= góc HBA
mà góc HED=góc CEK( đối đỉnh)=> góc HBA=góc CEK
lại có tam giác ABC vuông tại A=> góc HBA+ góc ECK=90 độ=> góc CEK+góc ECK=90 độ=>DK\(\perp AC\)
hay DE \(\perp AC\) mà CE\(\perp AD\)(tại H)=>E là trực tâm tam giác ADC
ăn cơm đã ý c tí mik làm sau

a: góc B=90-30=60 độ
góc B>góc C
=>AC>AB
góc CAH=90-30=60 độ>góc C
=>CH>AH
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
CH chung
HA=HD
=>ΔCAH=ΔCDH
c: Xét ΔACB và ΔDCB có
CA=CD
góc ACB=góc DCB
CB chung
=>ΔACB=ΔDCB
=>góc CDB=góc CAB=90 độ

a: ΔABC vuông tại A
b: góc B=2/3*90=60 độ
góc C=90-60=30 độ
Xét ΔABD có
AH vừa là đường cao, vừa là trung tuyến
góc B=60 độ
=>ΔABD đều
=>góc DAB=60 độ
=>góc DAC=góc DCA
=>DA=DC
Xét ΔDHA vuông tại H và ΔDEC vuông tại E có
DA=DC
góc ADH=góc CDE
=>ΔDHA=ΔDEC
=>DH=DE

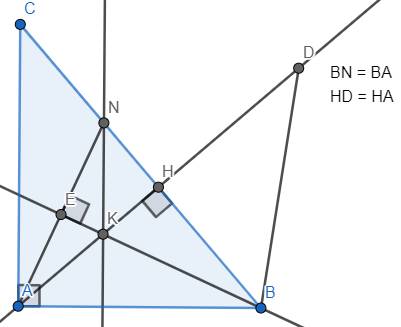
a) Xét ΔABE vuông tại E & ΔNBE vuông tại E có:
- BE là cạnh chung, BN = BA (giả thuyết)
Suy ra ΔABE = ΔNBE (cạnh huyền - cạnh góc vuông)
b) Theo đề ta có BH vuông góc với AD và HA = HD
Suy ra BH là đường trung trực của AD
Suy ra BA = BD (vì B nằm trên đường trung trực của AD)
c) Trong ΔNAB có AH và BE là đường cao, đồng quy tại điểm K
Suy ra NK là đường cao của ΔNAB, hay NK vuông góc với AB
Mà AC cũng vuông góc với AB, suy ra NK // CA
a. - Vì BE vuông góc với AN (gt)
=> tam giác ABE vuông tại E (tc)
tam giác NBE vuông tại E (tc)
- Xét tam giác vuông ABE và tam giác vuông NBE, có:
+ Chung BE
+ BA = BN (gt)
=> tam giác vuông ABE = tam giác vuông NBE (Cạnh huyền - cạnh góc vuông)
b. - Vì AH là đường cao của tam giác ABC (gt)
=> tam giác ABH vuông tại H
tam giác DBH vuông tại H
- Xét tam giác vuông ABH và tam giác vuông DBH, có:
+ Chung BH
+ HA = HD (gt)
=> tam giác vuông ABH = tam giác vuông DBH (2 cạnh góc vuông)
=> BA = BD (2 cạnh tương ứng)

Làm tiếp nha:
Xét tứ giác ABEC có 2 đường chéo AE và BC cắt nhau tại trung điểm M của mỗi đường nên ABEC là hình bình hành.
=> \(\hept{\begin{cases}AB=CE\left(1\right)\\ABllCE\end{cases}}\)
a ) xét \(\Delta ABM\)và \(\Delta ECM\)có:
\(\hept{\begin{cases}MA=ME\left(gt\right)\\MB=MC\left(gt\right)\\AB=CE\left(cmt\right)\end{cases}}\)
---> \(\Delta ABM=\Delta ECM\left(c.c.c\right)\)
b) Xét \(\Delta ABD\) có BH là đường cao đồng thời đường trung tuyến nên \(\Delta ABD\) cân tại B.
---> BC là phân giác của ABD
\(\Delta ABD\)cân tại B ---> AB = BD (2)
Từ (1),(2) ---> BD = CE

a, xét 2 t.giác vuông ABH và MBH có:
AH=MH(gt)
HB cạnh chung
=> t.giác ABH=t.giác MBH(cạnh góc vuông-cạnh góc vuông)
b, vì I là trung điểm của BC nên AI=1/2 BC<=> AI=IC
=>t.giác AIC cân tại I
xét 2 t.giác vuông ABC và CDA có:
AC cạnh chung
\(\widehat{ACB}\)=\(\widehat{CAD}\)(t.giác AIC cân tại I)
=>t.giác ABC=t.giác CDA(cạnh góc vuông-góc nhọn)
=> CD=AB(2 cạnh tương ứng)
c,dễ nên tự làm
a, xét 2 t.giác vuông ABH và MBH có:
AH=MH(gt)
HB cạnh chung
=> t.giác ABH=t.giác MBH(cạnh góc vuông-cạnh góc vuông)
b, vì I là trung điểm của BC nên AI=1/2 BC<=> AI=IC
=>t.giác AIC cân tại I
xét 2 t.giác vuông ABC và CDA có:
AC cạnh chung
góc ACB = góc CAD (t.giác AIC cân tại I)
=>t.giác ABC=t.giác CDA(cạnh góc vuông-góc nhọn)
=> CD=AB(2 cạnh tương ứng)
c) Ta có \(\hept{\begin{cases}\widehat{ACB+\widehat{ABC=90}độ}\\HBM+HMB=90\end{cases}}\)(do tam giác ABC zuông tại a , do tam giác BHM zuông tại H
mà ABH=HBM do ( Tam giác AHB=tam giác HBM cmt)
=> ACB=HMB hay ACB =AMB
4 năm nữa em trả lời nghen
giúp ik :(((