Cho đường tròn (O, R). Từ một điểm M nằm ngoài đường tròn tâm, kẻ hai tiếp tuyến MA, MB đến (O) (với A, B là các tiếp điểm). Qua A kẻ đường thẳng song song với MO cắt đường tròn tại E, đường thẳng ME cắt đường tròn tại F đường thẳng AF cắt MO tại N.
a) Chứng minh tứ giác MAOB nội tiếp đường tròn.
b) Chứng minh MN2 = NF.NA
c) Gọi H là giao điểm của MO và AB Chứng minh MN = NH và...
Đọc tiếp
Cho đường tròn (O, R). Từ một điểm M nằm ngoài đường tròn tâm, kẻ hai tiếp tuyến MA, MB đến (O) (với A, B là các tiếp điểm). Qua A kẻ đường thẳng song song với MO cắt đường tròn tại E, đường thẳng ME cắt đường tròn tại F đường thẳng AF cắt MO tại N.
a) Chứng minh tứ giác MAOB nội tiếp đường tròn.
b) Chứng minh MN2 = NF.NA
c) Gọi H là giao điểm của MO và AB Chứng minh MN = NH và (HB^2/HF^2)-(EF/MF)=1
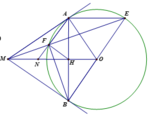
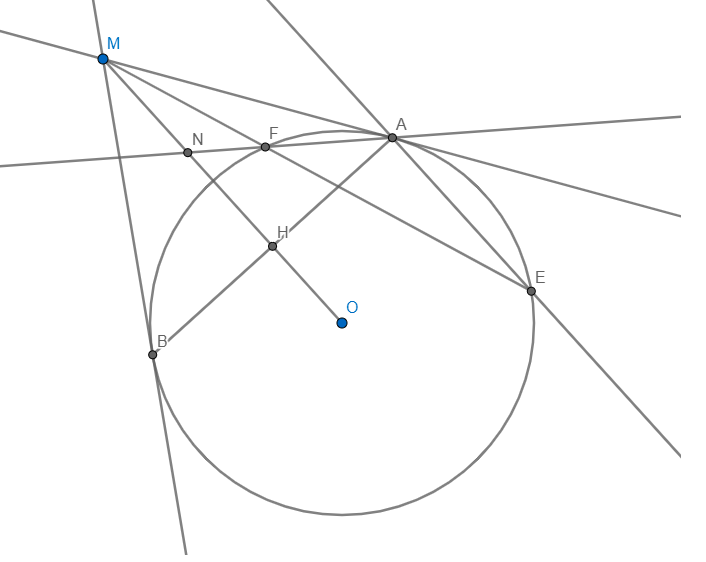
a: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
nên MAOB là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{MAF}\) là góc tạo bởi tiếp tuyến AM và dây cung AF
\(\widehat{AEF}\) là góc nội tiếp chắn cung AF
Do đó: \(\widehat{MAF}=\widehat{AEF}\)
mà \(\widehat{AEF}=\widehat{NMF}\)(hai góc so le trong, MN//AE)
nên \(\widehat{NMF}=\widehat{NAM}\)
Xét ΔNMF và ΔNAM có
\(\widehat{NMF}=\widehat{NAM}\)
\(\widehat{MNF}\) chung
Do đó: ΔNMF~ΔNAM
=>\(\dfrac{NM}{NA}=\dfrac{NF}{NM}\)
=>\(NM^2=NF\cdot NA\)