 help câu b hìnhhh
help câu b hìnhhh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(x+\dfrac{1}{4}=\dfrac{1}{5}\)
\(x=\dfrac{1}{5}-\dfrac{1}{4}\)
\(x=\dfrac{4}{20}-\dfrac{5}{20}\)
\(x=-\dfrac{1}{20}\)
b) \(x-\dfrac{1}{5}=\dfrac{3}{20}\)
\(x=\dfrac{3}{20}+\dfrac{1}{5}\)
\(x=\dfrac{3}{20}+\dfrac{4}{20}\)
\(x=\dfrac{7}{20}\)
c) \(\dfrac{5}{6}-x=1\)
\(x=\dfrac{5}{6}-1\)
\(x=\dfrac{5}{6}-\dfrac{6}{6}\)
\(x=-\dfrac{1}{6}\)

a: \(S_{ABC}=\dfrac{1}{2}\cdot4\cdot9=2\cdot9=18\left(cm^2\right)\)
b: Kẻ AH//DK(H thuộc BC)
=>H là trung điểm của CK
=>BK=2KH=2/3BH
mà BK=1/2BC
nên 2/3BH=1/2BC
=>BH=3/4BC
Xét ΔBAH có EK//AH
nên BK/BH=BE/BA=2/3
=>BE/BA=2/3
\(BC=\sqrt{4^2+9^2}=\sqrt{97}\left(cm\right)\)
\(sinB=\dfrac{AC}{BC}=\dfrac{4}{\sqrt{97}}\)
BK=1/2BC=căn 97/2
BE=2/3BA=6cm
\(S_{BEK}=\dfrac{1}{2}\cdot\dfrac{\sqrt{97}}{2}\cdot\dfrac{4}{\sqrt{97}}\cdot6=\dfrac{24}{4}=6\left(cm^2\right)\)
AE=1/3AB=3cm
\(S_{ADE}=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)=S_{BEK}\)


a: Xét ΔABD và ΔCBD có
BA=BC
\(\widehat{ABD}=\widehat{CBD}\)
BD chung
Do đó: ΔABD=ΔCBD
Suy ra: AD=CD

B) \(\dfrac{-11}{6}+\dfrac{2}{5}+\dfrac{-1}{6}+\dfrac{13}{5}=\left(\dfrac{-11}{6}-\dfrac{1}{6}\right)+\left(\dfrac{2}{5}+\dfrac{13}{5}\right)=\dfrac{-12}{6}+\dfrac{15}{5}=-2+3=-1\)
C) \(\dfrac{1}{7}+\dfrac{-1}{5}+\dfrac{-1}{7}+\dfrac{2}{-5}+\dfrac{-7}{5}=\left(\dfrac{1}{7}-\dfrac{1}{7}\right)+\left(\dfrac{-1}{5}-\dfrac{2}{5}-\dfrac{7}{5}\right)=0-\dfrac{10}{5}=0-2=-2\)
D) \(\dfrac{-5}{8}+\dfrac{12}{7}+\dfrac{13}{8}+\dfrac{2}{7}=\left(\dfrac{13}{8}-\dfrac{5}{8}\right)+\left(\dfrac{12}{7}+\dfrac{2}{7}\right)=\dfrac{8}{8}+\dfrac{14}{7}=12=3\)
E)\(\dfrac{1}{7}+\dfrac{-1}{5}+\dfrac{1}{-7}+\dfrac{2}{-5}+\dfrac{-7}{5}=\left(\dfrac{1}{7}-\dfrac{1}{7}\right)+\left(\dfrac{-1}{5}-\dfrac{2}{5}-\dfrac{7}{5}\right)=0-\dfrac{10}{5}=-2=-2\)
b: =(-11/6-1/6)+(2/5+13/5)
=-2+3
=1
c: =(3/13+10/13)+(-3/7-4/7)
=1-1=0
d: =(-5/8+13/8)+(12/7+2/7)
=-1+2
=1

a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
b: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA\(\perp\)BC tại H

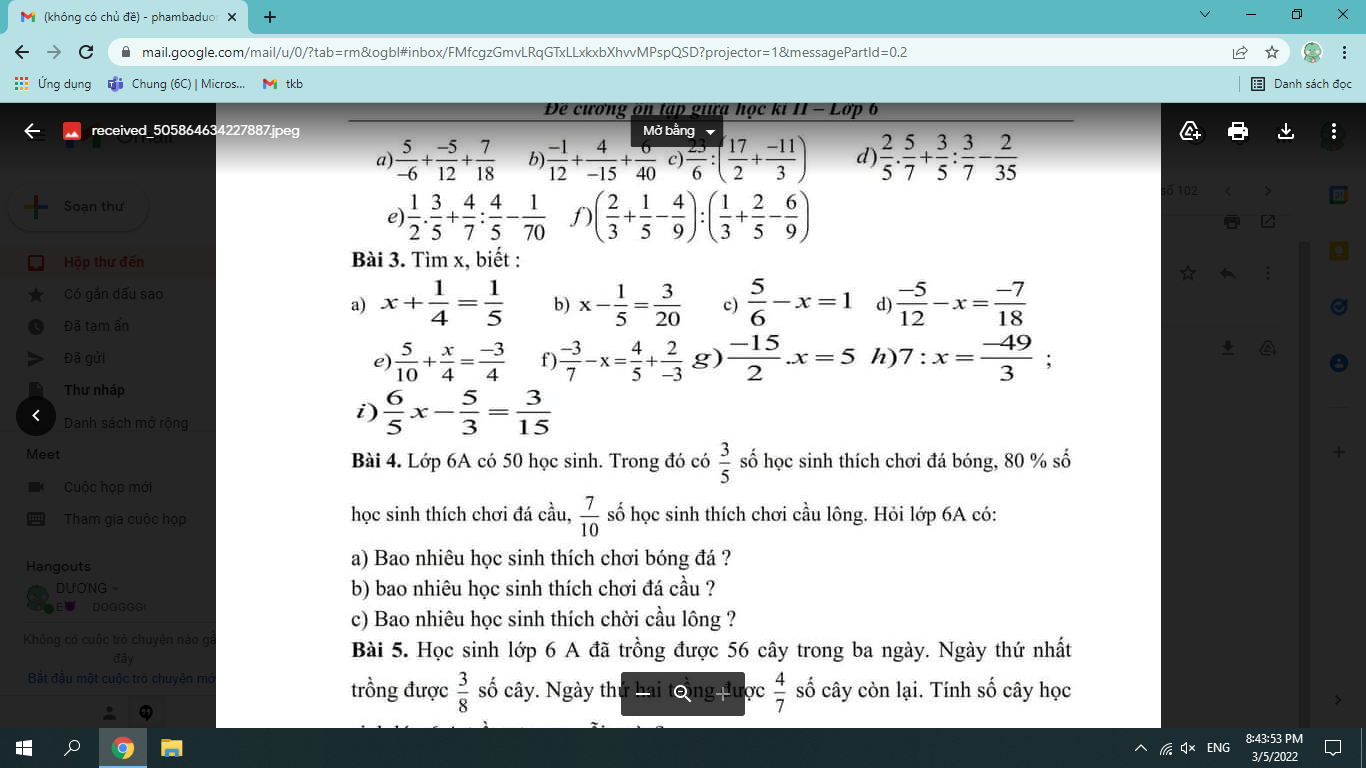 help bài 3 câu a ,b, và c help
help bài 3 câu a ,b, và c help

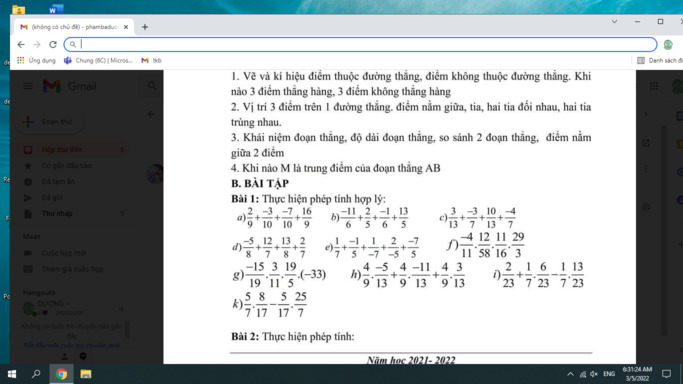 HELP CÂU B ,C,D,E,
HELP CÂU B ,C,D,E,


