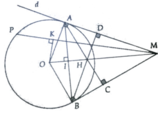
cho (O,R) điểm a nằm trên (O) gọi d là tiếp tuyến của (O) tại A, lấy M thuộc d (MA>R) kẻ tiếp tuyến MB của(O) ( B là tiếp điểm, B khác A)
a) CM 4 điểm O,A,M,B thuộc 1 đg tròn
b) tia đối BA lấy điểm C. Kẻ MH vuông góc OC tại H, AB cắt OM tại I
CM OM vuông góc AB
OH.OC=OI.OM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 5 2022
a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=180^0\)
nên MAOB là tứ giác nội tiếp(1)
Xét tứ giác OHMB có \(\widehat{OHM}+\widehat{OBM}=180^0\)
nên OHMB là tứ giác nội tiếp(2)
Từ (1) và (2) suy ra O,H,A,M,B cùng thuộc đường tròn
b: Xét ΔMAC và ΔMDA có
\(\widehat{MAC}=\widehat{MDA}\)
\(\widehat{AMC}\) chung
Do đó:ΔMAC\(\sim\)ΔMDA
Suy ra: MA/MD=MC/MA
hay \(MA^2=MD\cdot MC=MO^2-R^2\)
CM
4 tháng 7 2018
a, HS tự làm
b, Chú ý O K M ^ = 90 0 và kết hợp ý a) => A,M,B,O,K ∈ đường tròn đường kính OM
c, Sử dụng hệ thức lượng trong tam giác vuông OAM ( hoặc có thể chứng minh tam giác đồng dạng)
d, Chứng minh OAHB là hình bình hành và chú ý A,B thuộc (O;R) suy ra OAHB là hình thoi
e, Chứng minh OH ⊥ AB, OMAB => O,H,M thẳng hàng
30 tháng 11 2021
2: Xét tứ giác OBCD có
\(\widehat{OBC}+\widehat{ODC}=180^0\)
Do đó: OBCD là tứ giác nội tiếp
hay O,B,C,D cùng thuộc một đường tròn
29 tháng 4 2023
Sửa đề; AH vuông góc BC, I là trung điểm của AH, MO cắt AB tại K
a: A,E,B,C cùng thuộc (O)
=>góc AEB+góc ACB=180 dộ
=>góc AEK+góc KEB+góc ACB=180 độ
=>góc KEB=90 độ-góc ACB
góc KMB=90 độ-góc ABM
mà góc ABM=góc ACB
nên góc KEB=góc KMB
=>MEKB nội tiếp
=>góc EMK=góc EBK=góc EAM
=>OM là tiếp tuyến của đừog tròn ngoại tiếp ΔMEA
9 tháng 12 2023
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
DB,DM là các tiếp tuyến
Do đó: DB=DM
Xét (O) có
EM,EC là các tiếp tuyến
Do đó: EM=EC
Chu vi tam giác ADE là:
\(C_{ADE}=AD+DE+AE\)
\(=AD+DM+ME+AE\)
\(=AD+DB+CE+AE\)
\(=AB+AC=2\cdot AB\)
2 tháng 12 2023
a: ΔONP cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)NP tại K
Ta có: \(\widehat{OAM}=\widehat{OBM}=\widehat{OKM}=90^0\)
=>O,A,M,B,K cùng thuộc đường tròn đường kính OM
b: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của BA(1)
OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AI là đường cao
nên \(OI\cdot OM=OA^2=R^2\)
Xét ΔOAM vuông tại A có AI là đường cao
nên \(OI\cdot IM=IA^2\)
c: AC\(\perp\)BM
OB\(\perp\)BM
Do đó: OB//AC
=>OB//AH
BD\(\perp\)MA
OA\(\perp\)MA
Do đó: BD//OA
=>BH//OA
Xét tứ giác OBHA có
OB//HA
OA//HB
Do đó: OBHA là hình bình hành
Hình bình hành OBHA có OB=OA
nên OBHA là hình thoi
d: OBHA là hình thoi
=>OH là đường trung trực của BA
mà M nằm trên đường trung trực của BA(cmt)
nên O,H,M thẳng hàng
AH
Akai Haruma
Giáo viên
25 tháng 11 2023
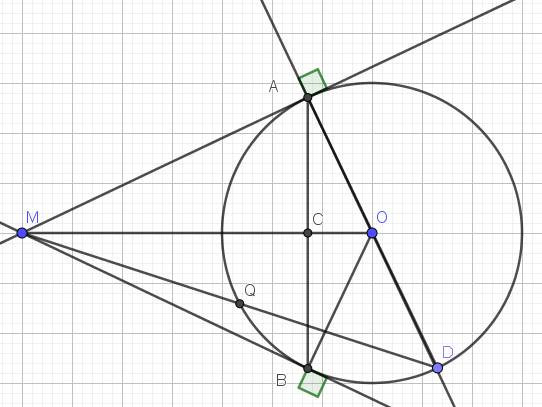
Lời giải:
1. Vì $MA, MB$ là tiếp tuyến của $(O)$ nên $MA\perp OA, MB\perp OB$.
Khi đó $\widehat{MAO}=\widehat{MBO}=90^0$
Tứ giác $MAOB$ có tổng 2 góc đối nhau $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$
$\Rightarrow MAOB$ là tứ giác nội tiếp.
$\Rightarrow M,A,O,B$ cùng thuộc 1 đường tròn.
2.
Có: $MA=MB, OA=OB$ nên $MO$ là trung trực của $AB$
$\Rightarrow MO\perp AB$ tại $C$.
Xét tam giác $MOB$ vuông tại $B$ có đường cao $BC$. Áp dụng hệ thức lượng trong tam giác vuông thì:
$MC.MO=MB^2(1)$
Xét tam giác $MQB$ và $MBD$ có:
$\widehat{M}$ chung
$\widehat{MBQ}=\widehat{MDB}$ (góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chắn cung đó)
$\Rightarrow \triangle MQB\sim \triangle MBD$ (g.g)
$\Rightarrow \frac{MQ}{MB}=\frac{MB}{MD}$
$\Rightarrow MQ.MD=MB^2(2)$
Từ $(1); (2)\Rightarrow MQ.MD=MC.MO$
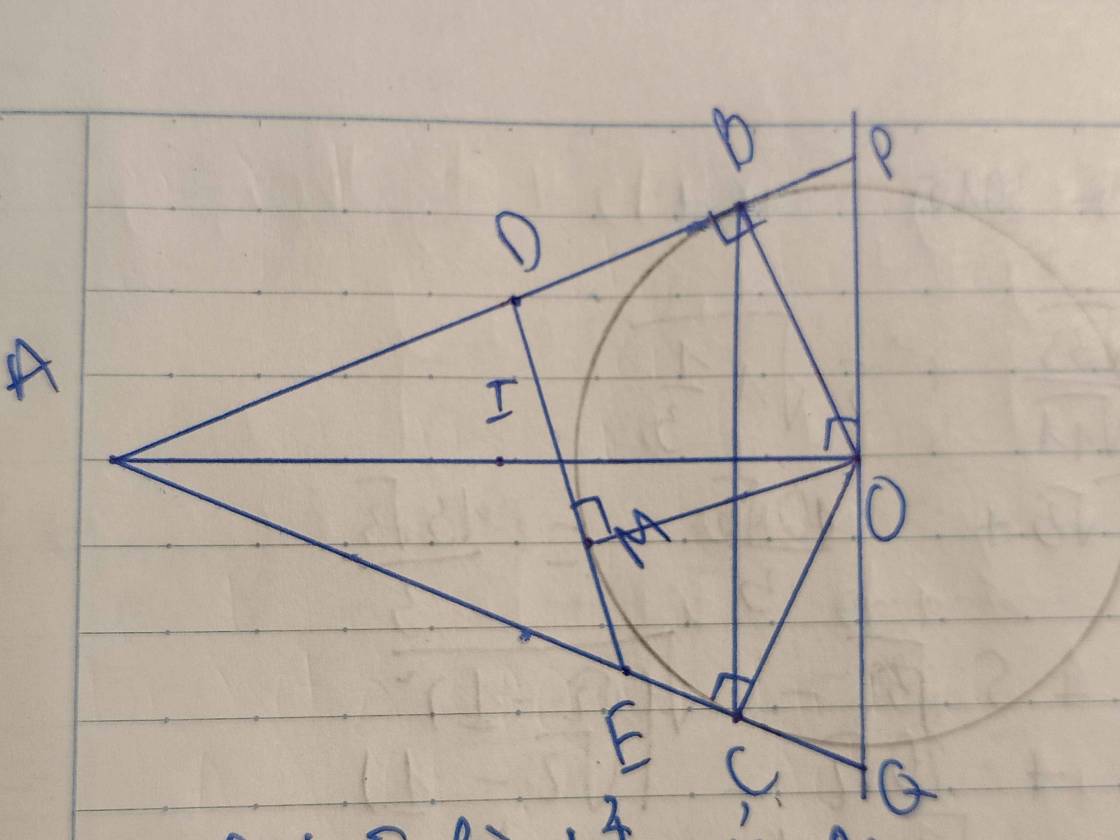
Lời giải:
a.
Do $MA, MB$ là tiếp tuyến của $(O)$ nên $MA\perp OA, MB\perp OB$
$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$
Tứ giác $MAOB$ có tổng hai góc đối $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$ nên $MAOB$ là tứ giác nội tiếp,
$\Rightarrow O,A,M,B$ cùng thuộc một đường tròn.
b.
Vì $MA, MB$ là tiếp tuyến của $(O)$ nên $MA=MB$
Mà: $OA=OB$
$\Rightarrow MO$ là trung trực của $AB$
$\Rightarrow MO\perp AB$ tại $I$
Vì $OM\perp AB$ tại $I$ nên $\widehat{MIC}=90^0$
$MH\perp OC$ tại $H$ nên $\widehat{MHC}=90^0$
Tứ giác $MIHC$ có $\widehat{MIC}=\widehat{MHC}=90^0$ và cùng nhìn cạnh $MC$ nên $MIHC$ là tứ giác nội tiếp.
$\Rightarrow \widehat{OMH}=\widehat{OCI}$
Xét tam giác $OMH$ và $OCI$ có:
$\widehat{O}$ chung
$\widehat{OMH}=\widehat{OCI}$
$\Rightarrow \triangle OMH\sim \triangle OCI$ (g.g)
$\Rightarrow \frac{OM}{OH}=\frac{OC}{OI}\Rightarrow OM.OI=OH.OC$
Hình vẽ: