tìm x thuộc N (2023^2024x+2023^2025x)/(2023^2023x+2023^2024x)=2023
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 8 2023
Có `xyz=2023=>2023=xyz`
Thay vào ta có :
\(\dfrac{xyz\cdot x}{xy+xyz\cdot x+xyz}+\dfrac{y}{yz+y+xyz}+\dfrac{z}{xz+z+1}=1\\ \dfrac{x^2yz}{xy\left(1+xz+z\right)}+\dfrac{y}{y\left(z+1+xz\right)}+\dfrac{z}{xz+z+1}=1\\ \dfrac{xz}{1+xz+z}+\dfrac{1}{z+1+xz}+\dfrac{z}{xz+z+1}=1\\ \dfrac{xz+1+z}{1+xz+z}=1\left(dpcm\right)\)
2 tháng 8 2023
`@` `\text {Ans}`
`\downarrow`
`(-2023) \times 33+2023 \times (-68)+2023`
`= 2023 \times (-33 - 68 + 1)`
`= 2023 \times (-101 + 1)`
`= 2023 \times (-100)`
`= -202300`
2 tháng 8 2023
-100 thì nhân với 2023 phải là -202300 mới đúng chứ ạ
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1
TH1: \(x+y+z+t=0\)
\(P=\left(1+\dfrac{x+y}{z+t}\right)^{2023}+\left(1+\dfrac{y+z}{x+t}\right)^{2023}+\left(1+\dfrac{z+t}{x+y}\right)^{2023}+\left(1+\dfrac{t+x}{y+z}\right)^{2023}\)
\(=\left(\dfrac{x+y+z+t}{z+t}\right)^{2023}+\left(\dfrac{x+y+z+t}{x+t}\right)^{2023}+\left(\dfrac{x+y+z+t}{x+y}\right)^{2023}+\left(\dfrac{x+y+z+t}{y+z}\right)^{2023}\)
\(=0+0+0+0=0\) là số nguyên (thỏa mãn)
TH2: \(x+y+z+t\ne0\), áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2023x+y+z+t}=\dfrac{y}{x+2023y+z+t}=\dfrac{z}{x+y+2023z+t}+\dfrac{t}{x+y+z+2023t}\)
\(=\dfrac{x+y+z+t}{\left(2023x+y+z+t\right)+\left(x+2023y+z+t\right)+\left(x+y+2023z+t\right)+\left(x+y+z+2023t\right)}\)
\(=\dfrac{x+y+z+t}{2026\left(x+y+z+t\right)}=\dfrac{1}{2026}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{2023x+y+z+t}=\dfrac{1}{2026}\\\dfrac{y}{x+2023y+z+t}=\dfrac{1}{2026}\\\dfrac{z}{x+y+2023z+t}=\dfrac{1}{2026}\\\dfrac{t}{x+y+z+2023t}=\dfrac{1}{2026}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2026x=2023x+y+z+t\\2026y=x+2023y+z+t\\2026z=x+y+2023z+t\\2026t=x+y+z+2023t\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}4x=x+y+z+t\\4y=x+y+z+t\\4z=x+y+z+t\\4t=x+y+z+t\end{matrix}\right.\)
\(\Rightarrow4x=4y=4z=4t\) (vì đều bằng \(x+y+z+t\))
\(\Rightarrow x=y=z=t\)
Do đó:
\(P=\left(1+\dfrac{x+x}{x+x}\right)^{2023}+\left(1+\dfrac{x+x}{x+x}\right)^{2023}+\left(1+\dfrac{x+x}{x+x}\right)^{2023}+\left(1+\dfrac{x+x}{x+x}\right)^{2023}\)
\(=2^{2023}+2^{2023}+2^{2023}+2^{2023}\)
\(=4.2^{2023}=2^{2025}\in Z\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1
Em kiểm tra lại đề, 2 ngoặc cuối bị giống nhau, chắc em ghi nhầm
14 tháng 9 2023
Xét VT : x+3x+5x+7x+......+2023x
Số hạng của dãy số trên là : \(\dfrac{2023-1}{2}+1=1012\left(sốhạng\right)\)
Tổng số của dãy số trên là : \(\dfrac{\left(2023x+x\right).1012}{2}\text{=}1012x.1012\)
Do đó : ta có :
\(1012x.1012\text{=}2023.2024\)
\(1012x\text{=}4046\)
\(x\text{=}\dfrac{2023}{506}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 9 2023
VT = x + 3x + 5x + 7x +... + 2023x = [(2023 - 1):2 +1] . (2023+1)x = 1012. 2024x = 2048288x
VP= 2023 . 2024= 4094552
VT=VP <=> 2048288x =4094552
<=>\(x\approx2\)
12 tháng 8 2023
\(\dfrac{x-2023}{6}+\dfrac{x-2023}{10}+\dfrac{x-2023}{15}+\dfrac{x-2023}{21}=\dfrac{8}{21}\)
\(\left(x-2023\right)\left(\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}\right)=\dfrac{8}{21}\)
\(\left(x-2023\right).\dfrac{8}{21}=\dfrac{8}{21}\)
\(x-2023=1\)
\(x=2024\)
Vậy..............
12 tháng 8 2023
\(...\Rightarrow\left(x-2023\right)\left(\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}\right)=\dfrac{8}{21}\)
\(\Rightarrow\left(x-2023\right)\left(\dfrac{35+21+14+1}{210}\right)=\dfrac{8}{21}\)
\(\Rightarrow\left(x-2023\right).\dfrac{71}{210}=\dfrac{8}{21}\)
\(\Rightarrow\left(x-2023\right).\dfrac{71}{210}=\dfrac{8}{21}.\dfrac{210}{71}=\dfrac{80}{71}\)
\(\Rightarrow x-2023=\dfrac{80}{71}\Rightarrow x=\dfrac{80}{71}+2023=\dfrac{143713}{71}\)
28 tháng 2 2023
\(y\times2023-y=2023\times2021+2023\)
\(y\times\left(2023-1\right)=2023\times\left(2021+1\right)\)
\(y\times2022=2023\times2022\)
\(y=2023\times2022\div2022\)
\(y=2023\)
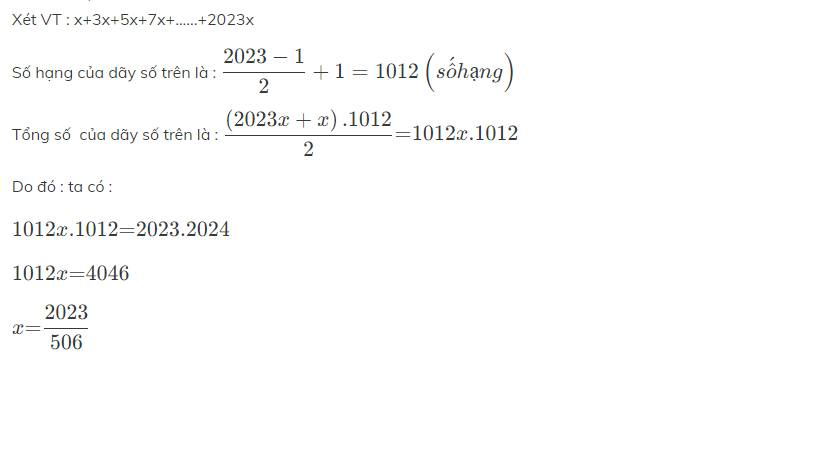
\(\dfrac{2023^{2024x}+2023^{2025x}}{2023^{2023x}+2023^{2024x}}=2023\)
=>\(\dfrac{2023^{2024x}\left(1+2023^x\right)}{2023^{2023x}\left(1+2023^x\right)}=2023\)
=>\(2023^x=2023\)
=>x=1