 CHo mình hỏi bài 2 với bài 3 ạ
CHo mình hỏi bài 2 với bài 3 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


i)\(\left\{{}\begin{matrix}ab=2\\a^3+b^3=9\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}ab=2\\\left(a+b\right)^3-3ab\left(a+b\right)=9\end{matrix}\right.\)
\(\Rightarrow\left(a+b\right)^3-6\left(a+b\right)-9=0\)
\(\Leftrightarrow\left(a+b\right)^3-3\left(a+b\right)^2+3\left(a+b\right)^2-9\left(a+b\right)+3\left(a+b\right)-9=0\)
\(\Leftrightarrow\left(a+b-3\right)\left[\left(a+b\right)^2+3\left(a+b\right)+3\right]=0\)
\(\Leftrightarrow a+b=3\)( \(\left(a+b\right)^2+3\left(a+b\right)+3>0;\forall a,b\)
ii) \(\left\{{}\begin{matrix}a+b+ab=23\\a^2+b^2=34\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}ab=23-\left(a+b\right)\\\left(a+b\right)^2-2ab=34\end{matrix}\right.\)
\(\Rightarrow\left(a+b\right)^2-2\left[23-\left(a+b\right)\right]=34\)
\(\Leftrightarrow\left(a+b\right)^2+2\left(a+b\right)-80=0\)
\(\Leftrightarrow\left(a+b-8\right)\left(a+b+10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=8\\a+b=-10\end{matrix}\right.\)

\(\dfrac{1}{3+0,5}+\dfrac{1}{3-0,5}\)
\(=\dfrac{3-0,5}{\left(3+0,5\right)\left(3-0,5\right)}+\dfrac{3+0,5}{\left(3+0,5\right)\left(3-0,5\right)}\)
\(=\dfrac{3-0,5+3+0,5}{3^2-\left(0,5\right)^2}\)
\(=\dfrac{6}{9-0,25}\)
\(=\dfrac{24}{35}\)

2 bài chiếm:
1-2/3-1/5=2/15
=>Tổng số bài là 2:2/15=15(bài)

tiêu đề bài hai có nghĩa là j zậy bnnnnnnnnnnnnnnnn
mk nhát đọc đề quá

a,mấy đoạn dấu : dấu+ trong đề hơi khó nhìn
\(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(P=\left[\dfrac{\sqrt{x}.\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\left(\dfrac{\sqrt{x}-1+2}{x-1}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{x-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}:\dfrac{1}{\sqrt{x}-1}=\dfrac{x-1}{\sqrt{x}}\)
b, \(P>0=>\dfrac{x-1}{\sqrt{x}}>0=>x-1>0< =>x>1\)(tm)
Vậy \(x>1\) .....
\(\)

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

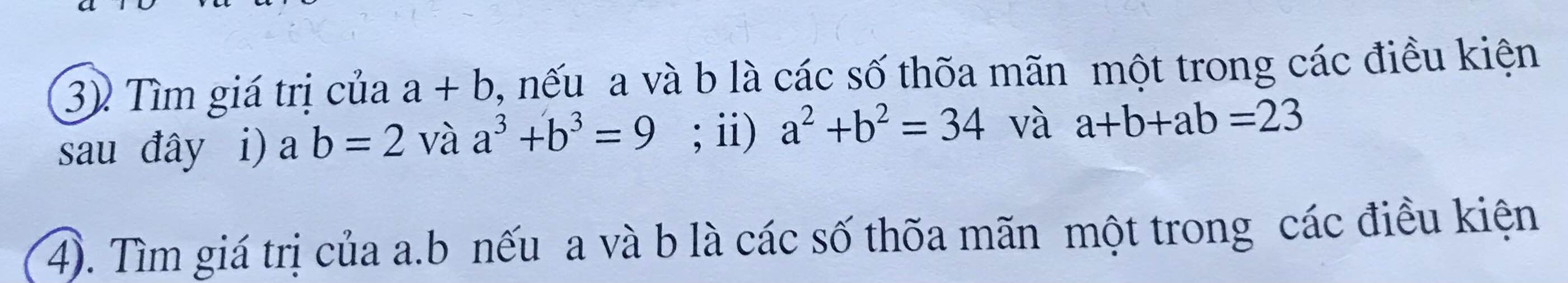
 bài 2, bài 3 ạ
bài 2, bài 3 ạ





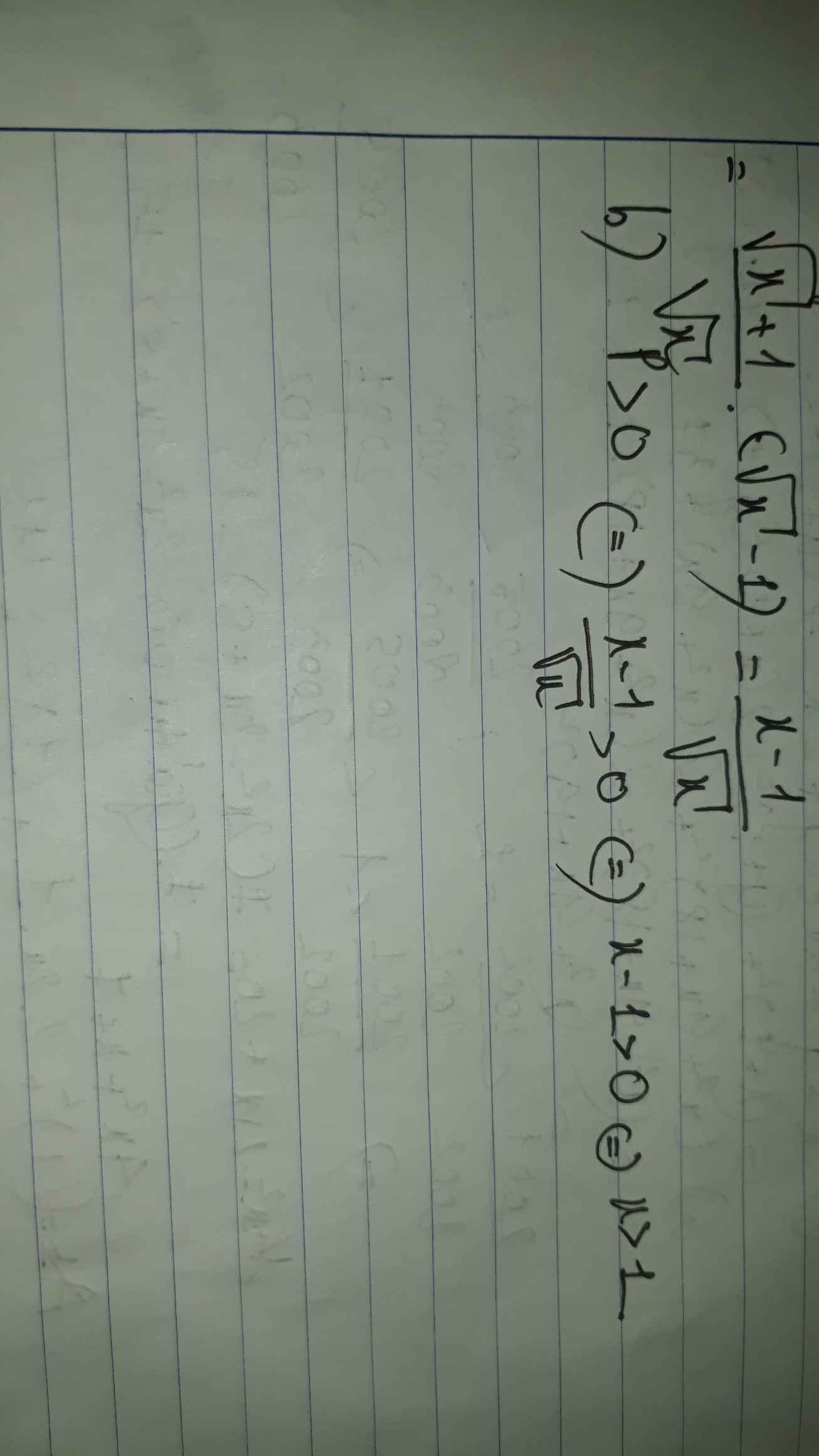




Bài 3:
Phương trình hoành độ giao điểm là:
\(x^2=3x-2\)
=>\(x^2-3x+2=0\)
=>(x-1)(x-2)=0
=>\(\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Khi x=1 thì \(y=1^2=1\)
Khi x=2 thì \(y=2^2=4\)
Vậy: (P) giao (d) tại A(1;1); B(2;4)
bài 2:
a: Thay x=2 vào y=-x+4, ta được:
\(y=-2+2=2=y_A\)
Vậy: A(2;2) thuộc (d)
b: Thay x=2 và y=2 vào y=ax2, ta được:
\(a\cdot2^2=2\)
=>4a=2
=>\(a=\dfrac{1}{2}\)
Khi a=1/2 thì (P): \(y=\dfrac{1}{2}x^2\)
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=-x+4\)
=>\(\dfrac{1}{2}x^2+x-4=0\)
=>\(x^2+2x-8=0\)
=>(x+4)(x-2)=0
=>\(\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)
Khi x=-4 thì \(y=-\left(-4\right)+4=8\)
Vậy: Giao điểm thứ hai là B(-4;8)
c: O(0;0); A(2;2); B(-4;8)
\(OA=\sqrt{\left(2-0\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(OB=\sqrt{\left(-4-0\right)^2+\left(8-0\right)^2}=4\sqrt{5}\)
\(AB=\sqrt{\left(-4-2\right)^2+\left(8-2\right)^2}=6\sqrt{2}\)
Vì \(OA^2+AB^2=OB^2\)
nên ΔAOB vuông tại A
=>\(S_{AOB}=\dfrac{1}{2}\cdot AB\cdot AO=\dfrac{1}{2}\cdot2\sqrt{2}\cdot6\sqrt{2}=12\)