Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi \(x\left(giờ\right),y\left(giờ\right)\) lần lượt là thời gian của đội thứ nhất và đội thứ hai làm riêng xong công việc (x, y > 0)
Trong một giờ hai đội làm được: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\) (công việc)
Đội thứ nhất làm trong 3 giờ rồi đội thứ hai làm tiếp trong 4 giờ được 0,8 công việc nên ta có:
\(\dfrac{3}{x}+\dfrac{4}{y}=0,8\)
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\\dfrac{3}{x}+\dfrac{4}{y}=0,8\end{matrix}\right.\)
Đặt \(u=\dfrac{1}{x};v=\dfrac{1}{y}\), ta có:
\(\left\{{}\begin{matrix}u+v=\dfrac{1}{4}\\3u+4v=0,8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4u+4v=1\\3u+4v=0,8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4u+4v=1\\u=\dfrac{1}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4.\dfrac{1}{5}+4v=1\\u=\dfrac{1}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}v=\dfrac{1}{20}\\u=\dfrac{1}{5}\end{matrix}\right.\)
*) \(u=\dfrac{1}{5}\Leftrightarrow\dfrac{1}{x}=\dfrac{1}{5}\Leftrightarrow x=5\) (nhận)
*) \(v=\dfrac{1}{20}\Leftrightarrow\dfrac{1}{y}=\dfrac{1}{20}\Rightarrow y=20\) (nhận)
Vậy đội thứ nhất làm riêng trong 5 giờ xong công việc
đội thứ hai làm riêng trong 20 giờ xong công việc
đổi 2 giờ 40 phút=\(\dfrac{8}{3}\) giờ
gọi thời gian đội 1 và đội 2 làm riêng để hoàn thành công việc lần lượt là
x,y(x,y>\(\dfrac{8}{3}\) )
=>hệ pt: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{\dfrac{8}{3}}=\dfrac{3}{8}\\y-x=4\end{matrix}\right.\) giải hệ pt trên ta được \(\left\{{}\begin{matrix}x=4\left(TM\right)\\y=8\left(TM\right)\end{matrix}\right.\)
vậy nếu làm riêng để hoàn thành công việc thì đội thứ nhất hết 4 giờ
đội thứ 2 hết 8 giờ
Bài giải:
Chiều rộng hình chữ nhật là:
12 : 4 = 3 ( dm)
Chu vi mảnh tấm bìa đó là:
( 12 + 3 ) x 2 = 30 ( dm)
Đáp số: 30dm.
Gọi x (giờ) là thời gian đội I làm một mình xong công việc (x > 12)
Thời gian đội thứ II làm một mình xong công việc là: x – 7 (giờ)
Trong một giờ đội I làm được 1/x (công việc)
Trong một giờ đội II làm được 1/(x-7) (công việc)
Trong một giờ cả hai đội làm được 1/12 (công việc)
Theo bài ra ta có phương trình:
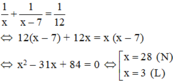
Vậy thời gian đội I làm xong công việc là 28 giờ, thời gian đội II làm xong công việc là: 28 – 7 = 21 (giờ)
Đáp án: C
TK:
1.
Gọi năng xuất làm việc trong 1 ngày của đội 1 và đội 2 lần lượt là:x và y(công việc/ngày).
2 đội công nhân cùng làm chung 1 công việc thì sau 15 ngày
⇒
15
×
y
+
15
×
y
=
1
(
1
)
Đội 1 làm riêng trong 3 ngày rồi dừng lại và đội 2 làm tiếp công việc đó trong 5 ngày thì cả 2 đội hoàn thành 25% công việc(ở đây mk đổi luôn)
⇒
3
×
x
+
5
×
y
=
1
4
⇒
5
×
(
3
×
x
+
5
×
y
)
=
5
×
1
4
15
×
x
+
25
×
y
=
5
4
(
2
)
Lấy (2) trừ đi (1) ta được:
(
15
×
x
+
25
×
y
)
−
(
15
×
x
+
15
×
y
)
=
5
4
−
1
10
×
y
=
1
4
y
=
1
4
:
10
⇒
y
=
1
40
⇒
x
=
1
24
Vậy .................
Tham Khảo:
1.
Gọi năng xuất làm việc trong 1 ngày của đội 1 và đội 2 lần lượt là:x và y(công việc/ngày).
2 đội công nhân cùng làm chung 1 công việc thì sau 15 ngày
⇒15×y+15×y=1(1)⇒15×y+15×y=1(1)
Đội 1 làm riêng trong 3 ngày rồi dừng lại và đội 2 làm tiếp công việc đó trong 5 ngày thì cả 2 đội hoàn thành 25% công việc(ở đây mk đổi luôn)
⇒3×x+5×y=14⇒3×x+5×y=14
⇒5×(3×x+5×y)=5×14⇒5×(3×x+5×y)=5×14
15×x+25×y=54(2)15×x+25×y=54(2)
Lấy (2) trừ đi (1) ta được:
(15×x+25×y)−(15×x+15×y)=54−1(15×x+25×y)−(15×x+15×y)=54−1
10×y=1410×y=14
y=14:10y=14:10
⇒y=140⇒y=140
⇒x=124⇒x=124
Vậy .................
Gọi x ( giờ ) là thời gian đội 1 làm một mình xong công việc ( x > 12 )
Thời gian đội thứ 2 làm một mình xong công việc là : \(x-7\left(giờ\right)\)
Trong một giờ đội 1 làm được \(\dfrac{1}{x}\left(\text{công việc}\right)\)
Trong một giờ đội 2 làm được \(\dfrac{1}{x-7}\left(\text{công việc}\right)\)
Trong một giờ cả hai đội làm được \(\dfrac{1}{12}\left(\text{công việc}\right)\)
Theo bài ra ta có pt : \(\dfrac{1}{x}+\dfrac{1}{x-7}=\dfrac{1}{12}\Leftrightarrow12\left(x-7\right)+12x=x\left(x-7\right)\Leftrightarrow x^2-31x+84=0\Leftrightarrow\left\{{}\begin{matrix}x=28\left(N\right)\\x=3\left(L\right)\end{matrix}\right.\)
Vậy thời gian đội 1 làm xong công việc là 8 giờ , thời gian đội 2 làm xong công việc là : \(28-7=21\left(giờ\right)\)
Giả sử nếu làm riêng thì người thứ nhất hoàn thành công việc trong x giờ, người thứ hai trong y giờ. Điều kiện x > 0, y > 0.
Trong 1 giờ người thứ nhất làm được 1/x công việc, người thứ hai 1/y công việc, cả hai người cùng làm chung thì được 1/8 công việc.
Ta được : \(\frac{1}{x}+\frac{1}{y}=\frac{1}{8}\)
Trong 3 giờ, người thứ nhất làm được 3/x công việc, trong 4 giờ người thứ hai làm được 4/y công việc, cả hai người làm được 4/5 công việc
Ta được\(\frac{3}{x}+\frac{4}{x}=\frac{4}{5}\)
Ta có hệ phương trình : \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{8}\\\frac{3}{x}+\frac{4}{x}=\frac{5}{4}\end{cases}}\)
Giải ra ta được x = \(\frac{35}{4}\), y = \(\frac{280}{3}\)
Vậy người thứ nhất 35/4 giờ, người thứ hai 280/3 giờ.
Gọi thời gian đội 1 (làm một mình) hoàn thành công việc là T1 (giờ).
Gọi thời gian đội 2 (làm một mình) hoàn thành công việc là T2 (giờ).
Ta cần tìm T1 và T2.
Mội giờ đội 1 sẽ hoàn thành được 1/T1 khối lượng công việc.
Mội giờ đội 2 sẽ hoàn thành được 1/T2 khối lượng công việc.
Và cả 2 đội 1 giờ sẽ hoàn thành (1/T1 + 1/T2) khối lượng công việc.
Vậy nếu 2 đội cùng làm thì thời gian để hoàn thành công việc sẽ là:
1/(1/T1 + 1/T2) = 8 Hay 1/T1 + 1/T2 = 1/8. (*)
Nếu đội 1 làm trong 7 giờ thì họ sẽ hoàn thành 7x(1/T1) khối lượng CV.
Đội 2 làm tiếp 4 giờ nữa, thì cả 2 đội sẽ làm được 7x(1/T1) + 4x(1/T2) khối lượng CV, và theo bài ra là 4/5 công việc.
Tức là: 7x(1/T1) + 4x(1/T2) =4/5 (**)
Kết hợp (*) và (**) ta có hệ PT:
1/T1 + 1/T2 = 1/8
7/T1 + 4/T2 = 4/5
Giải hệ PT trên ta được: T1=10 và T2=40 (giờ).