11.[(2x-1^3)-1]+37=1401
X=bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 4 2022
Gọi số cần thêm là x
Theo đề, ta có:
\(\dfrac{x+11}{x+37}=\dfrac{1}{3}\)
=>3x+33=x+37
=>2x=4
hay x=2
15 tháng 1 2018
-7-2x = 37-(-26)
Suy ra -7-2x=11
Suy ra -2x=11-7
Suy ra -2x=4
Suy ra 2x= -4
Suy ra x = -4 :2 =-2
CM
9 tháng 9 2019
Điều kiện: 1 ≤ x ≤ 3
bpt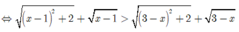 
Xét
f ( t ) = t 2 + 2 + t , t ≥ 0 f ' ( t ) = t 2 t 2 + 2 + 1 2 t , ∀ t > 0
Do đó hàm số đồng biến trên [ 0 ; + ∞ ) .
Từ (1) suy ra f(x-1) >f(3-x) hay x-1> 3-x
Suy ra : x> 2
So với điều kiện, bpt có tập nghiệm là S= (2; 3]
Do đó; a=2; b=3 và b-a=1
Chọn A.
CM
27 tháng 10 2019
Đáp án A
Điều kiện: 1 ≤ x ≤ 3 ; b p t ⇔ x − 1 2 + 2 + x − 1 > 3 − x 2 + 2 + 3 − x
Xét f t = t 2 + 2 + t với t ≥ 0 . Có f ' t = t 2 t 2 + 2 + 1 2 t > 0 , ∀ t > 0
Do đó hàm số đồng biến trên 0 ; + ∞ . 1 ⇔ f x − 1 > f 3 − x ⇔ x − 1 > 3 ⇔ x > 2
So với điều kiện, bpt có tập nghiệm là S = 2 ; 3
CM
7 tháng 3 2017
Điều kiện: 1≤ x≤ 3
Với điều kiện trên bpt
( x - 1 ) 2 + 2 + x - 1 > ( 3 - x ) 2 + 2 + 3 - x
Xét f ( t ) = t 2 + 2 + t v ớ i t ≥ 0
có f ' ( t ) = 1 2 t 2 + 2 + 1 2 t > 0 ∀ t > 0
Do đó hàm số đồng biến trên [0; +∞).
Khi đó (1) tương đương f(x-1) > f(3-x) hay x-1> 3-x
Suy ra x > 2
So với điều kiện, bpt có tập nghiệm là (2; 3] và 4a- b= 5
Chọn C.
CM
20 tháng 10 2019
Chọn đáp án A
Điều kiện: 1 ≤ x ≤ 3
Bất phương trình
(1)
Xét hàm số f t = t 2 + 2 + t với t ≥ 0
Ta có
nên hàm số đồng biến trên [ 0 ; + ∞ ) .
Khi đó (1) ⇔ f x - 1 > f 3 - x
Kết hợp với điều kiện, tập nghiệm của bất phương trình là S = ( 2 ; 3 ]
Vậy a = 2 , b = 3 ⇒ b - a = 1
KT
4
21 tháng 7 2018
3/8
13
Đặt tử ra ngoài rồi nhóm các phân số có mẫu lần lượt là 7,5,11,37 và tử là 1 vào xong rút gọn đi là ok = 3/4
\(11\times\left[\left(2x-1^3\right)-1\right]+37=1401\)
\(11\times\left[\left(2x-1\right)-1\right]=1401-37\)
\(\left(2x-1\right)-1=1364\div11\)
\(2x-1=124+1\)
\(2x=125+1\)
\(2x=126\)
\(\Rightarrow x=63\)
Chắc chắn đúng 100% luôn !
11[(2x-13)-1]+37=1401
=> 11[(2x-1)-1]=1401-37
=> 11[(2x-1)-1]=1364
=> (2x-1)-1=1364:11
=> (2x-1)-1=124
=> 2x-1=124+1
=> 2x-1=125
=> 2x=125+1
=> 2x=126
=> x=126:2
=> x=63