Tìm 3 nghiệm của phương trình x3 - 5x2 + 5x = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) 5x(x-2000)-x+2000=0
\(\Rightarrow5x\left(x-2000\right)-\left(x-2000\right)=0\\ \Rightarrow\left(x-2000\right)\left(5x-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x-2000=0\\5x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0+2000\\5x=0+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2000\\5x=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2000\\x=\dfrac{1}{5}\end{matrix}\right.\)

\(x^3-5x^2+2mx+5x-4m+2=0\)
\(\Leftrightarrow\left(x^3-5x^2+5x+2\right)+2m\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-3x-1\right)+2m\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-3x+2m-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x^2-3x+2m-1=0\left(1\right)\end{matrix}\right.\)
a. Pt đã cho có 3 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb khác 2
\(\Leftrightarrow\left\{{}\begin{matrix}4-6+2m-1\ne0\\\Delta=9-4\left(2m-1\right)>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{3}{2}\\m< \dfrac{13}{8}\end{matrix}\right.\)
b. Do vai trò 3 nghiệm như nhau, không mất tính tổng quát, giả sử \(x_1;x_2\) là nghiệm của (1) và \(x_3=2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=2m-1\end{matrix}\right.\)
\(x_1^2+x_2^2+x_3^2=11\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+4=11\)
\(\Leftrightarrow9-2\left(2m-1\right)-7=0\)
\(\Leftrightarrow m=1\)

5 x 2 + 4 x − x 2 − 3 x − 18 = 5 x 1
ĐK: 5 x 2 + 4 x ≥ 0 x 2 − 3 x − 18 ≥ 0 x ≥ 0 ⇔ x ≥ 0 , x ≤ − 4 5 x ≥ 6 , x ≤ − 3 x ≥ 0 ⇔ x ≥ 6
Khi đó 1 ⇔ 5 x 2 + 4 x = 5 x + x 2 − 3 x − 18
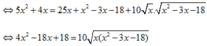
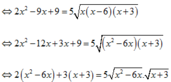
Dễ thấy x = 6 không là nghiệm phương trình nên với x > 6 ta chia cả hai vế cho x 2 − 6 x > 0 ta được:
2 + 3. x + 3 x 2 − 6 x = 5. x + 3 x 2 − 6 x 2
Đặt x + 3 x 2 − 6 x = t > 0 thì (2) trở thành 3 t 2 − 5 t + 2 = 0 ⇔ t = 1 ( T M ) t = 2 3 ( T M )
+ Nếu t = 1 thì x + 3 = x 2 − 6 x
⇔ x + 3 = x 2 − 6 x ⇔ x 2 − 7 x − 3 = 0 ⇔ x = 7 + 61 2 ( T M ) x = 7 − 61 2 ( L )
+ Nếu t = 2 3 thì x + 3 = 2 3 x 2 − 6 x ⇔ x + 3 = 4 9 ( x 2 − 6 x )
⇔ 4 x 2 − 33 x − 27 = 0 ⇔ x = 9 ( T M ) x = − 3 4 ( L )
Vậy phương trình đã cho có tập nghiệm s = 7 + 61 2 ; 9 hay S có 2 phần tử.
Đáp án cần chọn là: D

\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(4x^2-4x+1\right)+\left(y^2-2y+1\right)< 3\)
\(\Leftrightarrow\left(x-y\right)^2+\left(2x-1\right)^2+\left(y-1\right)^2< 3\)
\(\Rightarrow\left(2x-1\right)^2< 3\) (1)
\(\Rightarrow\left(2x-1\right)^2=\left\{0;1\right\}\)
\(\Rightarrow\left[{}\begin{matrix}2x-1=0\\2x-1=1\\2x-1=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
- Với \(x=0\Rightarrow2y^2-2y< 1\Rightarrow\left(2y-1\right)^2< 3\Rightarrow\left[{}\begin{matrix}y=0\\y=1\end{matrix}\right.\) (giải như (1))
- Với \(x=1\Rightarrow2y^2+5< 4y+5\Rightarrow y^2-2y< 0\)
\(\Rightarrow y\left(y-2\right)< 0\Rightarrow0< y< 2\Rightarrow y=1\)
Vậy \(\left(x;y\right)=\left(0;0\right);\left(0;1\right);\left(1;1\right)\)

Chọn A
Phương pháp:
- Tìm điều kiện xác định.
- Giải phương trình tìm nghiệm và tìm điều kiện để phương trình có nghiệm duy nhất.




Ta có:
\(P\left(x\right)=2x\left(x^3-3x+1\right)-\left(x^3-3x+1\right)+x^2-4\)
Do đó: \(P\left(a\right).P\left(b\right).P\left(c\right)=\left(a^2-4\right)\left(b^2-4\right)\left(c^2-4\right)\)
Ta có:
\(\left(x-a\right)\left(x-b\right)\left(x-c\right)=x^3-3x+1\)
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=0\\ab+ac+bc=-3\\abc=-1\end{matrix}\right.\)
C1: \(\left(a^2-4\right)\left(b^2-4\right)\left(c^2-4\right)=\left(abc\right)^2-4\left(a^2b^2+b^2c^2+c^2a^2\right)+16\left(a^2+b^2+c^2\right)-4^3\)
\(=1-4.9+16.6-4^3=-3\)\(\Rightarrow P\left(a\right).P\left(b\right).P\left(c\right)=-3\)
C2: Biến đổi thêm một chút
Ta có: \(a,b,c\ne0\) nên
\(a^3-3a+1=0\Leftrightarrow a\left(a^2-3\right)+1=0\)\(\Rightarrow a^2-3=\dfrac{-1}{a}\)
Tương tự...
\(\Rightarrow P\left(a\right).P\left(b\right).P\left(c\right)=\left(-\dfrac{1}{a}-1\right)\left(-\dfrac{1}{b}-1\right)\left(-\dfrac{1}{c}-1\right)\)
\(=-\left(\dfrac{1}{a}+1\right)\left(\dfrac{1}{b}+1\right)\left(\dfrac{1}{c}+1\right)\)\(=-\dfrac{a+1}{a}.\dfrac{b+1}{b}.\dfrac{c+1}{c}=abc+ac+bc+ab+a+b+c+1=-1-3+1=-3\)
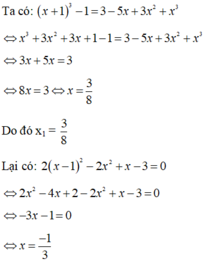
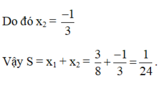
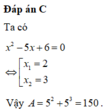


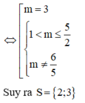
nhẩm được một nghiệm x=1
sử dụng sơ đồ hoocne