Cho tam giác ABC cân tại A. D là trung điểm của cạnh BC. Lấy điểm E bất kì thuộc cạnh BC. M,N lần lượt là chân đường vuông góc kẻ từ E đến các cạnh AB, AC. Chứng minh DM=DN.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TL
13 tháng 3 2023
a) Vì ΔABCΔ��� cân tại A(gt)�(��)
=> ˆABC=ˆACB���^=���^ (tính chất tam giác cân).
Mà ˆACB=ˆNCE���^=���^ (vì 2 góc đối đỉnh).
=> ˆABC=ˆNCE.���^=���^.
Hay ˆMBD=ˆNCE.���^=���^.
Xét 2 ΔΔ vuông BDM��� và CEN��� có:
ˆBDM=ˆCEN=900(gt)���^=���^=900(��)
BD=CE(gt)��=��(��)
ˆMBD=ˆNCE(cmt)���^=���^(���)
=> ΔBDM=ΔCENΔ���=Δ��� (cạnh góc vuông - góc nhọn kề).
=> DM=EN��=�� (2 cạnh tương ứng).
b) Xét 2 ΔΔ vuông DMI��� và ENI��� có:
ˆMDI=ˆNEI=900(gt)���^=���^=900(��)
DM=EN(cmt)��=��(���)
ˆDIM=ˆEIN���^=���^ (vì 2 góc đối đỉnh)
=> ΔDMI=ΔENIΔ���=Δ��� (cạnh góc vuông - góc nhọn kề).
=> MI=NI��=�� (2 cạnh tương ứng).
=> I là trung điểm của MN.��.
Mà I∈BC(gt)�∈��(��)
=> Đường thẳng BC�� cắt MN�� tại trung điểm I của MN(đpcm).��(đ���).
13 tháng 8 2021
a: Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
DB=CE
\(\widehat{MBD}=\widehat{NCE}\left(=\widehat{ACB}\right)\)
Do đó: ΔMBD=ΔNCE
Suy ra: DM=EN
2 tháng 1 2022
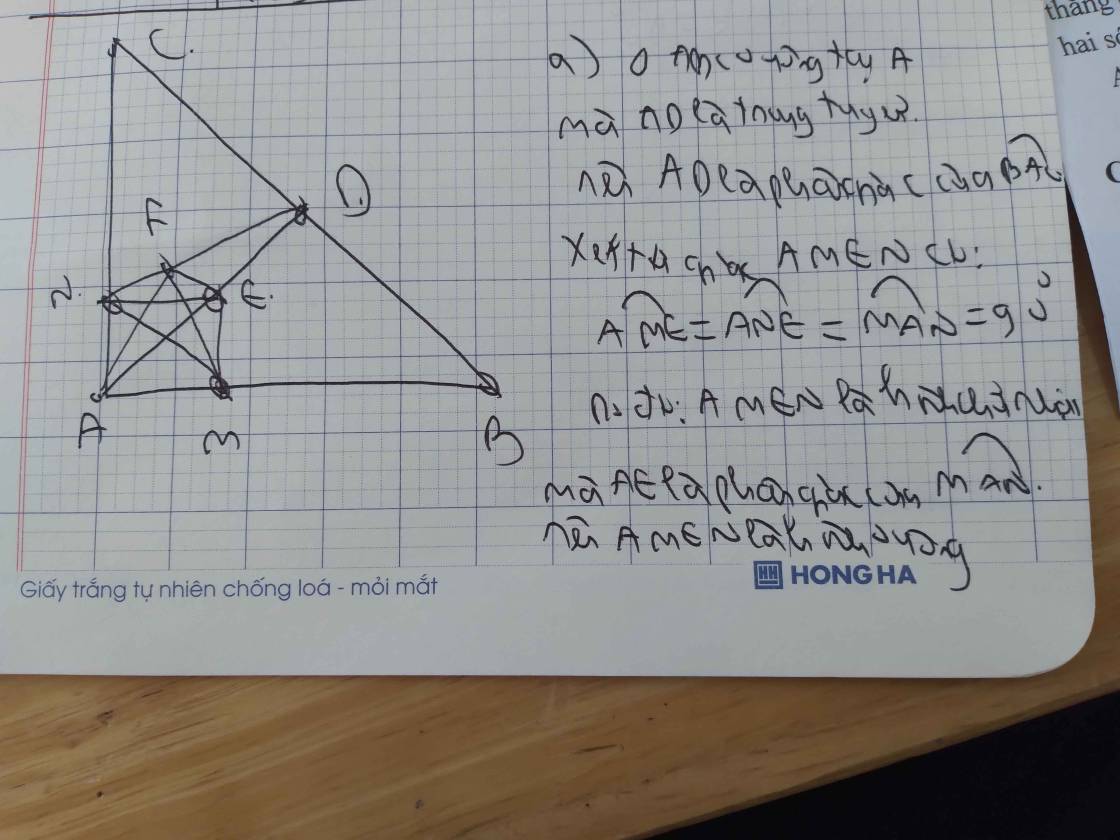
a: Xét tứ giác AMEN có
\(\widehat{AME}=\widehat{ANE}=\widehat{NAM}=90^0\)
Do đó: AMEN là hình chữ nhật
mà AE là tia phân giác
nen AMEN là hình vuông
28 tháng 10 2023
a: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là tia phân giác của \(\widehat{BAC}\)
Xét tứ giác AMEN có
\(\widehat{AME}=\widehat{ANE}=\widehat{MAN}=90^0\)
=>AMEN là hình chữ nhật
Hình chữ nhật AMEN có AE là phân giác của \(\widehat{MAN}\)
nên AMEN là hình vuông
b: AMEN là hình vuông
=>\(\widehat{AMN}=45^0\)
=>\(\widehat{AMN}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nênMN//BC
c: Gọi O là giao điểm của AE và MN
AMEN là hình vuông
=>AE cắt MN tại trung điểm của mỗi đường và AE=MN
=>O là trung điểm chung của AE và MN và AE=MN
=>\(OA=OE=OM=ON=\dfrac{MN}{2}=\dfrac{AE}{2}\)
ΔMFN vuông tại F
mà FO là đường trung tuyến
nên \(FO=\dfrac{MN}{2}=\dfrac{AE}{2}\)
Xét ΔAFE có
FO là đường trung tuyến
\(FO=\dfrac{AE}{2}\)
Do đó: ΔAFE vuông tại F
=>\(\widehat{AFE}=90^0\)
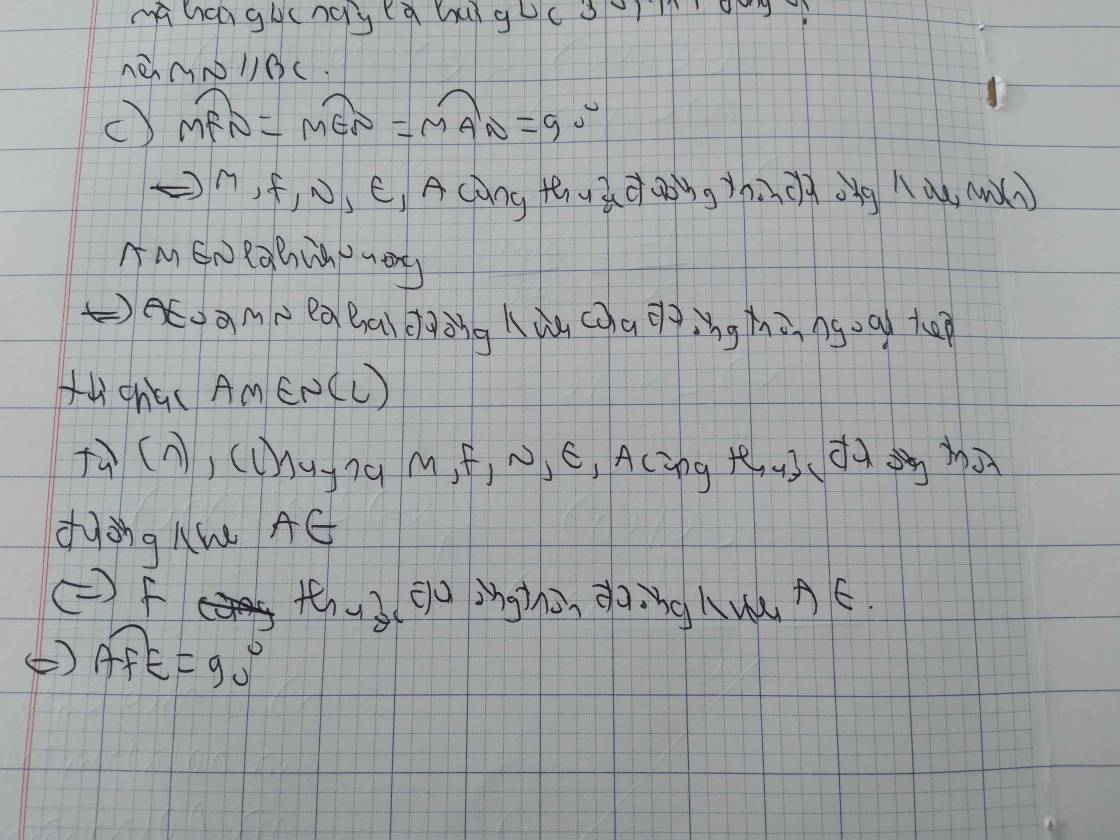
Gọi O là trung điểm của AE
Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là phân giác của góc BAC và AD\(\perp\)BC
=>\(\widehat{BAD}=\widehat{CAD}\left(3\right)\)
Vì \(\widehat{AME}=\widehat{ADE}=\widehat{ANE}=90^0\)
nên A,M,E,D,N cùng thuộc đường tròn đường kính AE
=>A,M,E,D,N cùng thuộc (O)
Xét (O) có
\(\widehat{DMN}\) là góc nội tiếp chắn cung DN
\(\widehat{DAN}\) là góc nội tiếp chắn cung DN
Do đó: \(\widehat{DMN}=\widehat{DAN}\)(1)
Xét (O) có
\(\widehat{DNM}\) là góc nội tiếp chắn cung DM
\(\widehat{DAM}\) là góc nội tiếp chắn cung DM
Do đó: \(\widehat{DNM}=\widehat{DAM}\left(2\right)\)
Từ (1),(2),(3) suy ra \(\widehat{DMN}=\widehat{DNM}\)
=>DM=DN
Đề sai. Bạn xem lại đề.