Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số \(N\left( t \right) = \frac{{25t + 10}}{{t + 5}},t \ge 0\), trong đó N(t) được tính bằng nghìn người.
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
b) Tính đạo hàm N’(t) và \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right)\). Từ đó giải thích tại sao dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua một ngưỡng nào đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chu kỳ của sóng \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{\pi }{{10}}}} = 20\;\left( s \right)\)
b) Vì \( - 1 \le \cos \left( {\frac{\pi }{{10}}t} \right) \le 1\;\;\;\;\; \Rightarrow - 90 \le 90\cos \left( {\frac{\pi }{{10}}t} \right) \le 90\)
Vậy chiều cao của sóng theo phương thẳng đứng là: \(90 + 90 = 180\;\left( {cm} \right)\)

a, Năm 2020, số dân VN là \(77,7+1,07\cdot20=99,1\left(tr.người\right)\)
Năm 2030, số dân VN là \(77,7+1,07\cdot30=109,8\left(tr.người\right)\)
b, VN đạt 115,15 tr người \(\Leftrightarrow115,15=77,7+1,07t\)
\(\Leftrightarrow37,45=1,07t\\ \Leftrightarrow t=35\)
Vậy vào năm 2035 thì thỏa mãn đề

Mấy câu trả lời SGK trình bày giúp anh Latex cái hoặc gõ ra nhưng gõ định dạng ấy em. Chứ như thế này anh sợ nhiều người không đọc được chữ ấy, mặc dù anh cũng đọc được.
Ta có:
\(\begin{array}{l}P'\left( t \right) = \frac{{{{\left( {500t} \right)}^\prime }\left( {{t^2} + 9} \right) - \left( {500t} \right){{\left( {{t^2} + 9} \right)}^\prime }}}{{{{\left( {{t^2} + 9} \right)}^2}}}\\ = \frac{{500\left( {{t^2} + 9} \right) - \left( {500t} \right).2t}}{{{{\left( {{t^2} + 9} \right)}^2}}}\\ = \frac{{500{t^2} + 4500 - 1000{t^2}}}{{{{\left( {{t^2} + 9} \right)}^2}}} = \frac{{4500 - 500{t^2}}}{{{{\left( {{t^2} + 9} \right)}^2}}}\end{array}\)
Tốc độ tăng dân số tại thời điểm \(t = 12\) là: \(P'\left( {12} \right) = \frac{{4500 - 500{t^2}}}{{{{\left( {{t^2} + 9} \right)}^2}}} \approx - 2,88\).

Dân số Việt Nam năm 2030 vào khoảng:
\(S=98564407\cdot e^{0,93\%\cdot9}=107169341\left(người\right)\)

Dân số của nước này sau 20 năm là;
\(A=19\cdot2^{\dfrac{20}{30}}\simeq30\)(triệu người)

a) Công thức tính dân số của tỉnh đó: \({S_n} = {u_1}{.1,01^n}\)
b) Dân số của tính đó sau 10 năm:
\({S_{10}} = {2.1,01^{10}} \approx 2,21\) (triệu dân)

a: Khối lượng của vật thời điểm t=0 là: \(m\left(0\right)=13\cdot e^{-0.015\cdot0}=13\left(kg\right)\)
b: Sau 45 ngày khối lượng còn lại là;
\(m\left(45\right)=13\cdot e^{-0.015\cdot45}\simeq6,62\left(kg\right)\)

Để tìm số trẻ mới sinh, chúng ta sẽ tính tích phân tỉ lệ sinh b(t) trên khoảng thời gian 10 năm đầu tiên sau chiến tranh
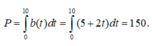
Vậy số trẻ được sinh cần tìm là 150 triệu.
Chọn đáp án C.
a) Dân số của thị trấn đó vào năm 2000 là: \(N\left( 0 \right) = \frac{{25.0 + 10}}{{0 + 5}} = \frac{{10}}{5} = 2\) (nghìn người)
Dân số của thị trấn đó vào năm 2015 là: \(N\left( {15} \right) = \frac{{25.15 + 10}}{{15 + 5}} = 19,25\) (nghìn người)
b) Ta có: , \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{25t + 10}}{{t + 5}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{25 + \frac{{10}}{t}}}{{1 + \frac{5}{t}}} = 25\)
Vì \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right) = 25\) và nên dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua ngưỡng 25 nghìn người.