một cỗ bài tú lơ khơ có 52 quân bài, chia số bài trên thành 4 phần bằng nhau, mỗi phần 13 quân. hỏi có bao nhiêu cách chia đc 1 phần sao cho:
a. có 2 con át
b. có ít nhất 1 con át
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu là kết quả của việc chọn ngẫu nhiên 4 con trong số 52 con
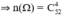
a. Đặt A : « Cả 4 con lấy ra đều là át »
⇒ n(A) = 1
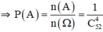
b. + B : « Không có con át nào trong 4 con khi lấy ra »
⇒ B là kết quả của việc chọn ngẫu nhiên 4 con trong số 48 con còn lại
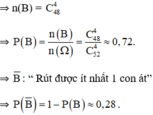
c. C: “Rút được 2 con át và 2 con K”.
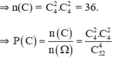

n(Ω) = C552 = 2598960 ( cách )
gọi biến cố đối của biến cố A la ' trong năm quân bài này ko có quân át '
➩ n(A đối) = 1712304 (cách )
➩ P(A đối) = n(A)/n(Ω) = 1712304/2598960 ( cách )
từ đó, suy ra P(A) = 1- P(A đối ) = 1-1712304/2598960 = 0,3412

Phép thử T được xét là: "Từ cỗ bài tú lơ khơ 52 con bài, rút ngẫu nhiên 4 con bài".
Mỗi kết quả có thể có là một tổ hợp chập 4 của 52 con bài. Do đó số các kết quả có thể có của phép thử T là n(Ω) = C452 = = 270725.
Vì rút ngẫu nhiên nên các kết quả có thể có là đồng khả năng.
a) Gọi biến cố A: "Rút được bốn con át". Ta có, số kết quả có thể có thuận lợi cho A là n(A) = 1. Suy ra P(A) = ≈ 0,0000037.
b) Gọi biến cố B: "Rút được ít nhất một con át". Ta có
= "Rút được 4 con bài đều không là át". Mỗi kết quả có thể thuận lợi cho
là một tổ hợp chập 4 của 48 con bài không phải là át. Suy ra số các kết quả có thể có thuận lợi cho
là C448 =
= 194580. Suy ra P(
) =
≈ 0,7187.
Qua trên ta có P(B) = 1 - P() ≈ 0,2813.
c) Gọi C là biến cố: "Rút được hai con át và hai con K".
Mỗi kết quả có thể có thuận lợi cho C là một tổ hợp gồm 2 con át và 2 con K. Vận dụng quy tắc nhân tính được số các kết quả có thể có thuận lợi cho C là
n(C) = C24 C24 = 6 . 6 = 36.
Suy ra P(C) = ≈ 0,000133.

Chia 13 quân cho người thứ nhất: \(C_{52}^{13}\) cách
Còn lại 39 quân, chia 13 quân cho người thứ 2: \(C_{39}^{13}\) cách
Còn lại 26 quân, chia 13 quân cho người thứ 3: \(C_{26}^{13}\) cách
Còn lại 13 quân, chia cho người thứ 4: \(C_{13}^{13}\) cách
\(\Rightarrow C_{52}^{13}.C_{39}^{13}.C_{26}^{13}.C_{13}^{13}\) cách

ta có: bộ bài có 52 quân 4 chất, mỗi chất 13 quân. vậy chất cơ có 13 quân, chất bích có 13 quân, chất tép có 1 quân, chất rô có 13 quân
để lấy đc 4 quân mà đc 4 chất khác nhau thì có số cách lấy là:\(C^1_4.C_{13}^1.C^1_3.C^1_{13}.C^1_2C_{13}^1.C^1_1.C^1_{13}\)
do 4 chất thì quân đầu tiên ta có \(C^1_4\)cách chọn chất và \(C_{13}^1\) cách chọn quân
tương tự với quân 2 ,3 và 4 .

Kí hiệu A k : Lần thứ k lấy được con át , k ≥ 1 . Rõ ràng A 1 , A 2 độc lập.
a) Ta cần tính P ( A 1 ∩ A 2 ) .
Ta có:
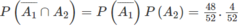
b) Theo bài ra ta cần tính:
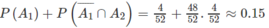
bài này đi thi toán nâng cao lớp 5 cũng có dạng như này
giải nhanh dùm e ạ