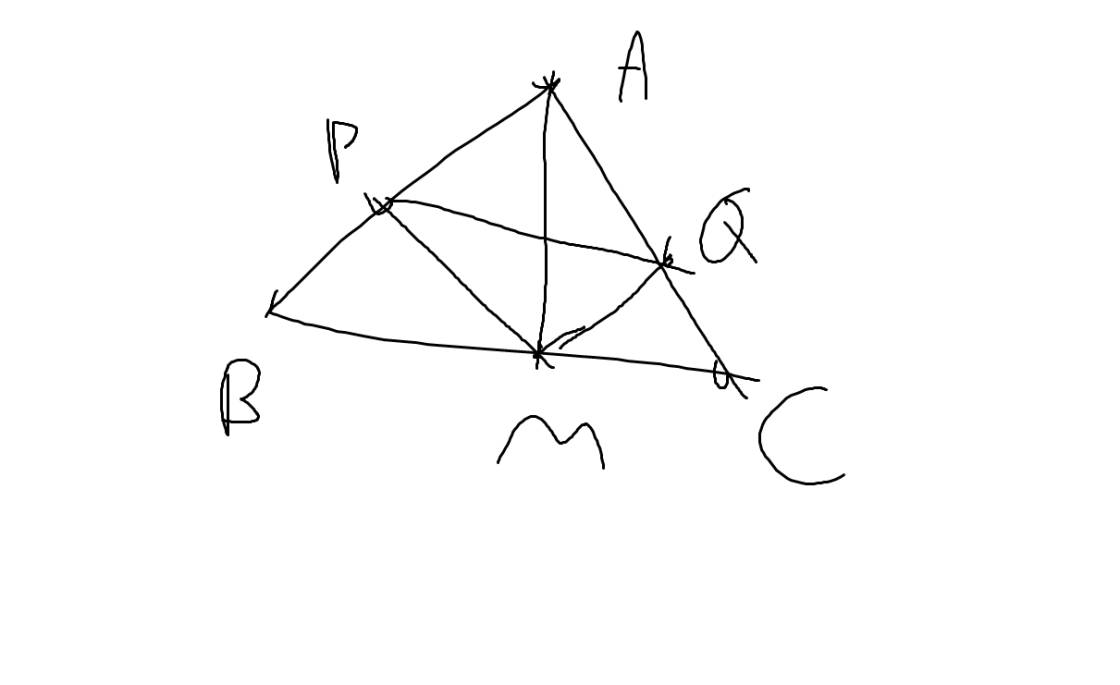
Cho tam giác ABC cân tại A (AB>BC), có hai đường chéo BE, CF và M là điểm bất kì trên BC. Vẽ Mp vuông góc AB tại P, MQ vuông góc AC tại Q. Trên tia đối của tia MQ lấy N sao cho MN=MP. Chứng minh:
a/ BEQN là hình chữ nhật
b/ MP+MQ=CF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔPAM vuông tại P và ΔQAM vuông tại Q có
AM chung
\(\widehat{PAM}=\widehat{QAM}\)
Do đó: ΔPAM=ΔQAM
=>PA=QA và MP=MQ
b: AP=AQ
=>A nằm trên đường trung trực của PQ(1)
MP=MQ
=>M nằm trên đường trung trực của PQ(2)
Từ (1) và (2) suy ra AM là đường trung trực của PQ
=>AM\(\perp\)PQ

tự kẻ hình nha
a) Vì M là trung điểm AB, PM=MQ, P,M,Q thẳng hàng=> M là trung điểm PQ
=>PQ giao AB tại trung điểm mỗi đường=> APBQ là hbh mà AB vuông góc với PQ=> APBQ là hình thoi
b) vì APBQ là hình thoi=> PB//AQ mà PB//CE=> CE//AQ (1)
ta có PQ vuông góc với AB
AC vuông góc với AB
=> AC//PQ=> EQ//AC ( PQ cắt đường thẳng // với PB tại E=> E thuộc PQ)(2)
từ (1);(2)=> ACEQ là hbh
c) 1) trong tam giác ABC có
MN //AC( N thuộc MP)
AM=MB
=> MN là đtb của tam giác => MN=AC/2=> AC=2MN
2) Vì AC=2MN=> AC=6cm
MN là đtb=> CN=BN
tam giác ABC vuông tại A
=> AN=BN=CN=BC/2( tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
=> BC=2AN=10cm
vì tam giác ABC vuông tại A=> AB^2+AC^2=BC^2
=> AB^2=100-36
=> AB=8 (AB>0)
=> chu vi tam giác ABC là 6+8+10=24(cm)

a: Xét ΔFBC vuông tại F và ΔECB vuông tại E có
BC chung
\(\widehat{FBC}=\widehat{ECB}\)
DO đó: ΔFBC=ΔECB
Suy ra: FB=EC
b: Ta có: AF+FB=AB
AE+EC=AC
mà BF=CE
và AB=AC
nên AF=AE
Xét ΔABC có AF/AB=AE/AC
nên FE//BC