 bài 5 ạ
bài 5 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 9:
Để A là số nguyên thì \(4x-10⋮x-2\)
=>\(4x-8-2⋮x-2\)
=>\(-2⋮x-2\)
=>\(x-2\inƯ\left(-2\right)\)
=>\(x-2\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{3;1;4;0\right\}\)
Bài 8:
Diện tích mảnh vườn là:
\(\dfrac{1}{2}\cdot10\cdot\left(15+25\right)=5\cdot40=200\left(m^2\right)\)
Khối lượng thóc thu được là:
\(200:1\cdot0,7=140\left(kg\right)\)
Bài 7:
\(\dfrac{2}{3}\cdot\left(\dfrac{1}{15}-\dfrac{5}{7}\right)+\dfrac{2}{3}+\dfrac{2}{3}\cdot\left(\dfrac{14}{15}+\dfrac{19}{7}\right)\)
\(=\dfrac{2}{3}\left(\dfrac{1}{15}-\dfrac{5}{7}+1+\dfrac{14}{15}+\dfrac{19}{7}\right)\)
\(=\dfrac{2}{3}\left(1+1+2\right)\)
\(=\dfrac{2}{3}\cdot4=\dfrac{8}{3}\)
Bài 6:
\(\left(-x+0,2\right)^3=0,008\)
=>\(-x+0,2=\sqrt[3]{0,008}=0,2\)
=>-x=0
=>x=0
=>Có 1 giá trị x thỏa mãn
Câu 4:
\(\left(\dfrac{2x}{3}-3\right):\left(-10\right)=\dfrac{2}{5}\)
=>\(x\cdot\dfrac{2}{3}-3=\dfrac{2}{5}\cdot\left(-10\right)=-4\)
=>\(x\cdot\dfrac{2}{3}=-4+3=-1\)
=>\(x=-1:\dfrac{2}{3}=-\dfrac{3}{2}\)

4.2:
a: x^2-x+1=x^2-x+1/4+3/4
=(x-1/2)^2+3/4>=3/4>0 với mọi x
=>x^2-x+1 ko có nghiệm
b: 3x-x^2-4
=-(x^2-3x+4)
=-(x^2-3x+9/4+7/4)
=-(x-3/2)^2-7/4<=-7/4<0 với mọi x
=>3x-x^2-4 ko có nghiệm
5:
a: x^2+y^2=25
x^2-y^2=7
=>x^2=(25+7)/2=16 và y^2=16-7=9
x^4+y^4=(x^2)^2+(y^2)^2
=16^2+9^2
=256+81
=337
b: x^2+y^2=(x+y)^2-2xy
=1^2-2*(-6)
=1+12=13
x^3+y^3=(x+y)^3-3xy(x+y)
=1^3-3*1*(-6)
=1+18=19

Bài 2
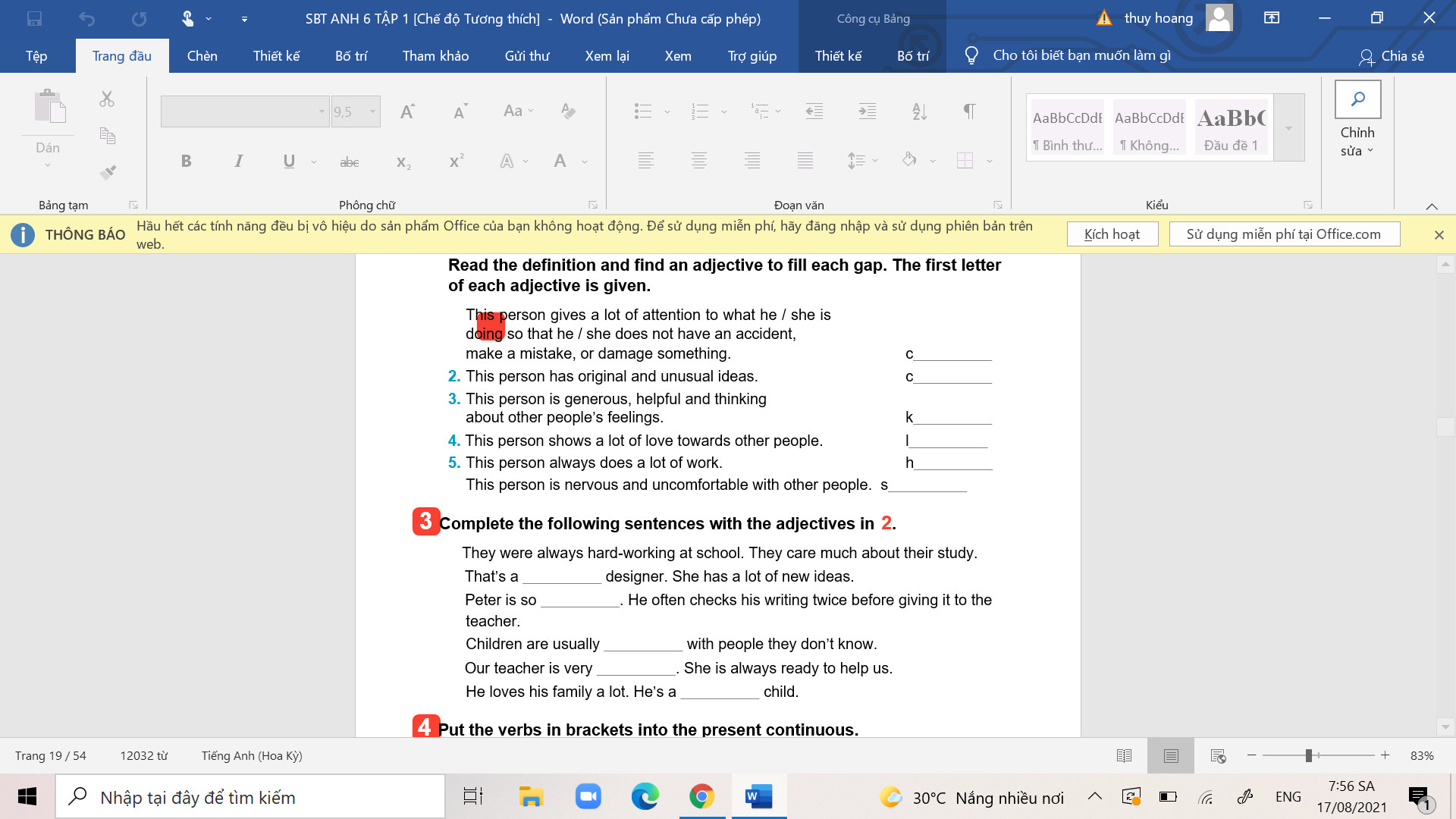
1 a lot of
2 much
3 a lot of - many
4 many
5 much
Bài 3
1 much
2 much
3 a lot of
4 lots of
5 many
Bài 4
1 much
2 many
3 a lot of
4 many
5 lots of
Bài 5
1 any - a - many
3 any
4 lots
5 many - lot
6 lot - any
III
1 desks
2 students
3 televisions
4 couches
5 bookshelves

Câu 5:
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: Xét tứ giác AEDF có
\(\widehat{EAF}=\widehat{AFD}=\widehat{AED}=90^0\)
Do đó: AEDF là hình chữ nhật
mà AD là tia phân giác của \(\widehat{FAE}\)
nên AEDF là hình vuông


b6 fashion - long hours - contacted - clients - grades
b5 c làm ở dưới r í

Bài 4:
\(a,\Rightarrow5⋮x\Rightarrow x\inƯ\left(5\right)=\left\{1;5\right\}\\ b,\Rightarrow x-2+7⋮x-2\\ \Rightarrow x-2\inƯ\left(7\right)=\left\{1;7\right\}\\ \Rightarrow x\in\left\{3;9\right\}\\ c,\Rightarrow3\left(x+1\right)+4⋮x+1\\ \Rightarrow x+1\inƯ\left(4\right)=\left\{1;2;4\right\}\\ \Rightarrow x\in\left\{0;1;3\right\}\\ d,\Rightarrow10x+6⋮2x-1\\ \Rightarrow5\left(2x-1\right)+11⋮2x-1\\ \Rightarrow2x-1\inƯ\left(11\right)=\left\{1;11\right\}\\ \Rightarrow x\in\left\{1;6\right\}\\ e,\Rightarrow x\left(x+3\right)+11⋮x+3\\ \Rightarrow x+3\inƯ\left(11\right)=\left\{1;11\right\}\\ \Rightarrow x=8\left(x\in N\right)\\ f,\Rightarrow x\left(x+3\right)+2\left(x+3\right)+5⋮x+3\\ \Rightarrow x+3\inƯ\left(5\right)=\left\{1;5\right\}\\ \Rightarrow x=2\left(x\in N\right)\)

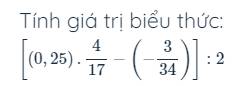
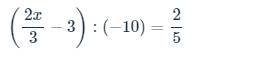
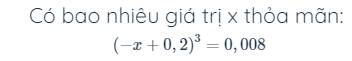
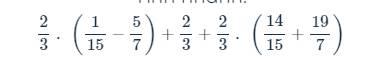

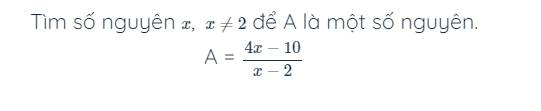







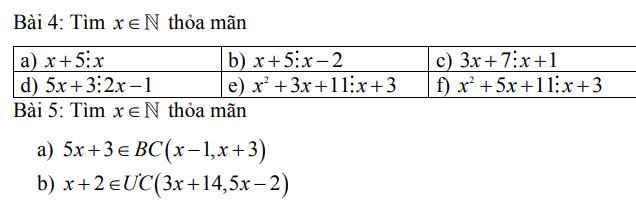
 các bn giúp mình bài 2, bài 3.
các bn giúp mình bài 2, bài 3.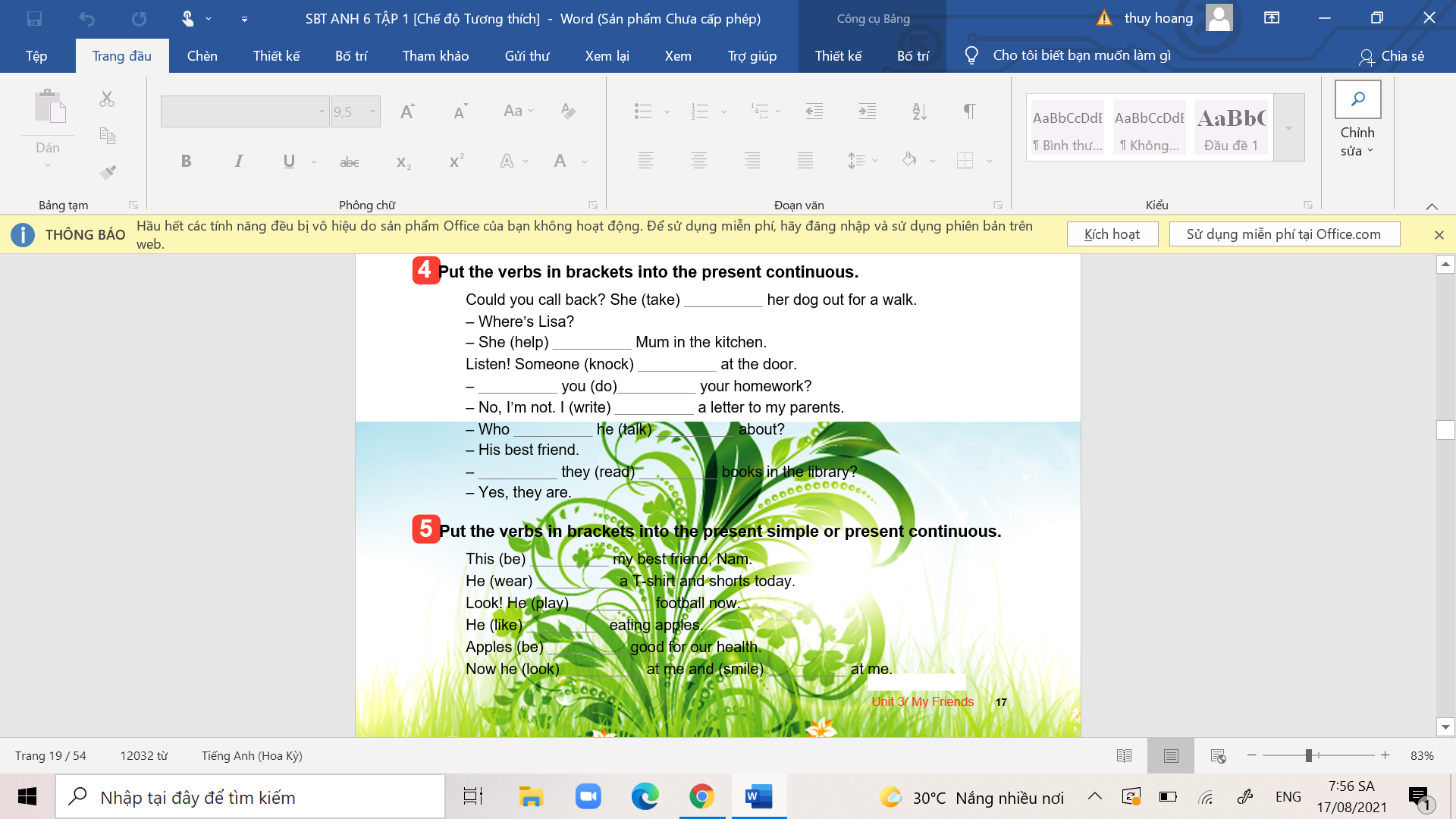 các bn giúp mình bài 4 và bài 5 nhé.
các bn giúp mình bài 4 và bài 5 nhé. 




Giải:
Sử dụng phương pháp giả thiết tạm
Giả sử mỗi đề tài chỉ có một người làm và không ai trùng đề tài thì số người tham gia là:
1 x 2 = 2 (người); loại Vì 2 < 6
Nếu có một đề tài có ít nhất hai người cùng trao đổi thì số người tham gia là:
2 x 1 + 1 = 3 (người); loại vì 3 < 6
Nếu có hai đề tài mỗi đề tài có ít nhất hai người cùng trao đổi thì số người tham gia là:
2 x 2 = 4 (người); loại vì 4 < 6
Vậy chắc chắn có 1 đề tài có ít nhất 3 người cùng trao đổi.