Cho hai đường thẳng (d): x+2y-1=0 và d’: x-3y+2=0.Số đo góc giữa hai đường thẳng là:
A,600
B,900
C,69034''
D,450
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
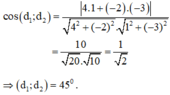

- Xét d1 và d2 có : \(\left\{{}\begin{matrix}\overrightarrow{n_{d1}}\left(1;-3\right)\\\overrightarrow{n_{d2}}\left(1;-2\right)\end{matrix}\right.\)
\(\Rightarrow\cos\alpha=\left|\dfrac{\overrightarrow{n_{d1}}.\overrightarrow{n_{d2}}}{\left|\overrightarrow{n_{d1}}\right|.\left|\overrightarrow{n_{d2}}\right|}\right|=\left|\dfrac{1.1+\left(-2\right).\left(-3\right)}{\sqrt{\left(1^2+\left(-3\right)^2\right)\left(1^2+\left(-2\right)^2\right)}}\right|=\dfrac{7\sqrt{2}}{10}\)
\(\Rightarrow\alpha=~8^o\)
- Từ d1 và d2 ta có hệ phương trình \(\left\{{}\begin{matrix}x-3y=-1\\x-2y=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=17\\y=6\end{matrix}\right.\)
Vậy tọa độ giao điểm của d1 và d2 là ( 17; 6 ) .

Áp dụng công thức cos =
ta có cos =
=> cos =
=
=
=>
= 450

\(d_1\) nhận \(\overrightarrow{n_1}=\left(1;2\right)\) là 1 vtpt
\(d_2\) nhận \(\overrightarrow{n_2}=\left(2;-1\right)\) là 1 vtpt
Do \(\overrightarrow{n_1}.\overrightarrow{n_2}=1.2+2.\left(-1\right)=0\Rightarrow d_1\perp d_2\)
hay góc giữa 2 đường thẳng là 90 độ

a) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}} = \left( {1;3} \right),\overrightarrow {{n_2}} = \left( {1; - 2} \right)\)
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {1.1 + 3.( - 2)} \right|}}{{\sqrt {{1^2} + {3^2}} \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} }} \approx 0,93 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) \approx 22^\circ 8'\)
b) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}} = \left( {4; - 2} \right),\overrightarrow {{n_2}} = \left( {2; - 1} \right)\)
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {4.2 + ( - 2).( - 1)} \right|}}{{\sqrt {{4^2} + {{\left( { - 2} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = 1 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) = 0^\circ \)
c) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}} = \left( {2; - 1} \right),\overrightarrow {{n_2}} = \left( {1;2} \right)\)
Ta có \({a_1}{a_2} + {b_1}{b_2} = 2.1 + ( - 1).2 = 0\)
Suy ra \(\left( {{\Delta _1},{\Delta _2}} \right) = 90^\circ \)

Vecto pháp tuyến của đường thẳng \({d_1}\) là: \(\overrightarrow {{n_1}} = \left( {2; - 1} \right)\)
Vecto pháp tuyến của đường thẳng \({d_2}\) là: \(\overrightarrow {{n_2}} = \left( {1; - 3} \right)\)
Ta có: \(\cos \left( {{d_1},{d_2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {2.1 + \left( { - 1} \right).\left( { - 3} \right)} \right|}}{{\sqrt {{{\left( 2 \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{\sqrt 2 }}{2}\)
Vậy \(\left( {{d_1},{d_2}} \right) = {45^o}\)

Đáp án D
Gọi I là giao điểm của hai đường thẳng d1; d2 . Tọa độ điểm I là nghiệm của hệ:
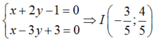
Lấy điểm m 1 ; 0 ∈ d 1 . Đường thẳng qua M và vuông góc với d2 có phương trình: 3x + y-3= 0
Gọi H = ∆ ∩ d 2 suy ra tọa độ điểm H là nghiệm của hệ:
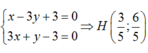
Phương trình đường thẳng
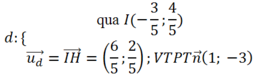
có dạng:
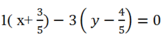
hay x-3y + 3= 0
cos(d,d')=\(\dfrac{\left|1.1+2.\left(-3\right)\right|}{\sqrt{1^2+2^2}.\sqrt{1^2+\left(-3\right)^2}}\)= \(\dfrac{\sqrt{2}}{2}\)=450