Hãy tìm các góc trong tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=54^0\)
Xét ΔABC vuông tại A có
\(AB=BC\cdot\sin36^0\)
nên \(AB\simeq4,11\left(cm\right)\)
\(\Leftrightarrow AC\simeq5,67\left(cm\right)\)

Gọi số đo các góc A,B,C lần lượt là a,b,c
Theo đề, ta co: \(\dfrac{180-a}{3}=\dfrac{180-b}{4}=\dfrac{180-c}{5}\)
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{180-a}{3}=\dfrac{180-b}{4}=\dfrac{180-c}{5}=\dfrac{180+180+180-a-b-c}{3+4+5}=\dfrac{540-180}{12}=\dfrac{360}{12}=30\)
=>180-a=90; 180-b=120; 180-c=150
=>a=90; b=60; c=30
Gọi số đo các góc trong tam giác `ABC` lần lượt là `x,y,z (x,y,z \ne 0)`
Gọi số đo các góc ngoài tam giác `ABC` lần lượt là `a, b, c (a,b,c \ne 0)`
Các góc ngoài đỉnh `A, B, C` lần lượt tỉ lệ với các số `3:4:5`
Nghĩa là: \(\dfrac{180-a}{3}=\dfrac{180-b}{4}=\dfrac{180-c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{180-a}{3}=\dfrac{180-b}{4}=\dfrac{180-c}{5}=\dfrac{180-a+180-b+180-c}{3+4+5}\)
\(=\dfrac{570-180}{12}=\dfrac{360}{12}=30\)
`->`\(\dfrac{180-x}{3}=\dfrac{180-y}{4}=\dfrac{180-z}{5}=30\)
`-> a=30*3=90, b=30*4=120, c=30*5=150`
`->`\(\left\{{}\begin{matrix}x=180^0-90^0=90^0\\y=180^0-120^0=60^0\\z=180^0-150^0=30^0\end{matrix}\right.\)
Vậy, các góc trong tam giác `ABC` lần lượt là `90^0, 60^0, 30^0.`

Ta có A = 180o - 70o - 45o = 65o.
Vì góc C là góc nhỏ nhất nên cạnh AB nhỏ nhất. Chọn A

a: góc A=90-60=30 độ
Xét ΔABC vuông tại A có sin C=AB/AC
=>6/AC=sin60
=>AC=4*căn 3(cm)
=>BC=2*căn 3(cm)
b; S ABC=1/2*2căn 3*6=6căn 3(cm2)

ta có AB = 8cm;AC=6cm;BC=9cm
suy ra BC>AB>AC(1)
Mà cạnh đối diện với cạnh lớn hơn thì lớn hớn , đối diện với cạnh nhỏ hơn thì nhỏ hơn(2)
AB đối diện với góc C (3)
BC đối diện với góc A(4)
AC đối diện với góc B(5)
Từ (1), (2), (3), (4), (5) suy ra A>C>B

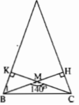
+) Xét tam giác vuông BKM có ∠BMC là góc ngoài tam giác tại đỉnh M nên:

Đặt \(\widehat{A}=a;\widehat{B}=b;\widehat{C}=c\)
Số đo góc A bằng 6 lần số đo góc B bằng 3 lần số đo góc C
=>a=6b=3c
=>\(\dfrac{a}{6}=\dfrac{6b}{6}=\dfrac{3c}{6}\)
=>\(\dfrac{a}{6}=\dfrac{b}{1}=\dfrac{c}{2}\)
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(a+b+c=180^0\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{1}=\dfrac{c}{2}=\dfrac{a+b+c}{6+1+2}=\dfrac{180}{9}=20\)
=>\(a=20\cdot6=120;b=1\cdot20=20;c=2\cdot20=40\)
Vậy: \(\widehat{A}=120^0;\widehat{B}=20^0;\widehat{C}=40^0\)
Lời giải:
Ta có: $\widehat{A}+\widehat{B}+\widehat{C}=180^0$ (tổng 3 góc trong 1 tam giác)
Áp dụng TCDTSBN:
$\widehat{A}=6\widehat{B}=3\widehat{C}=\frac{\widehat{A}}{1}=\frac{\widehat{B}}{\frac{1}{6}}=\frac{\widehat{C}}{\frac{1}{3}}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{1+\frac{1}{6}+\frac{1}{3}}=\frac{180^0}{\frac{3}{2}}=120^0$
$\Rightarrow \widehat{A}=120^0; \widehat{B}=120^0:6=20^0; \widehat{C}=120^0:3=40^0$