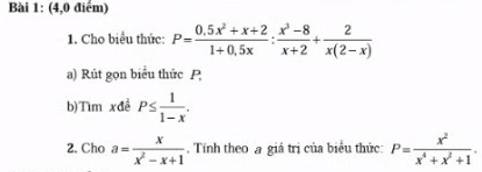
TYSM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`2^(x-1) + 2^x +2^(x+1) = 112 `
`=> 2^(x-1) + 2^(x-1) xx 2 +2^(x-1) xx 2^2 = 112 `
`=> 2^(x-1) . (1 + 2 + 2^2) = 112 `
`=> 2^(x-1) . 7 = 112 `
`=> 2^(x-1) = 16`
`=> 2^(x-1) = 2^4`
`=> x - 1 = 4`
`=> x = 5`

3ˣ⁺¹ + 3ˣ⁺³ = 810
3ˣ⁺¹.(1 + 3²) = 810
3ˣ⁺¹.10 = 810
3ˣ⁺¹ = 810 : 10
3ˣ⁺¹ = 81
3ˣ⁺¹ = 3⁴
x + 1 = 4
x = 4 - 1
x = 3

Lời giải:
$A-4=1+4+4^2+4^3+...+4^{2008}$
$4(A-4)=4+4^2+4^3+...+4^{2009}$
$\Rightarrow 4(A-4)-(A-4)=4^{2009}-1$
$\Rightarrow 3(A-4)=4^{2009}-1$
$\Rightarrow 3A=4^{2009}+11> 4^{2009}=4.4^{2008}$
$\Rightarrow A> \frac{4.4^{2008}}{3}> 4^{2008}$
$\Rightarrow 2A> 2.4^{2008}> 4^{2006}$ hay $2A> B$
Hay $A> \frac{B}{2}$
Đề sai bạn xem lại.

1) Áp dụng định lí pytago vào \(\Delta\)ABC vuông tại A, ta được
BC2=AB2+AC2
hay BC2=32+42=25
\(\Rightarrow\)\(BC=\sqrt{25}=5cm\)
Vậy: Khi AB=3cm; AC=4cm thì BC=5cm
2)
Áp dụng định lí pytago vào \(\Delta\)ABC vuông tại A, ta được
BC2=AB2+AC2
hay BC2=82+62=100
\(\Rightarrow\)\(BC=\sqrt{100}=10cm\)
Vậy: Khi AB=8cm; AC=6cm thì BC=10cm

1:
a: ĐKXĐ: \(x\notin\left\{-2;2;0\right\}\)
\(\dfrac{0,5x^2+x+2}{1+0,5x}:\dfrac{x^3-8}{x+2}+\dfrac{2}{x\left(2-x\right)}\)
\(=\dfrac{0,5\left(x^2+2x+4\right)}{0,5\left(x+2\right)}\cdot\dfrac{x+2}{\left(x-2\right)\left(x^2+2x+4\right)}-\dfrac{2}{x\left(x-2\right)}\)
\(=\dfrac{1}{x-2}-\dfrac{2}{x\left(x-2\right)}=\dfrac{x-2}{x\left(x-2\right)}=\dfrac{1}{x}\)
b: \(P< =\dfrac{1}{1-x}\)
=>\(\dfrac{1}{x}< =\dfrac{1}{1-x}\)
=>\(\dfrac{1}{x}-\dfrac{1}{1-x}< =0\)
=>\(\dfrac{1-x-x}{x\left(1-x\right)}< =0\)
=>\(\dfrac{2x-1}{x\left(x-1\right)}< =0\)
TH1: \(\left\{{}\begin{matrix}2x-1< =0\\x\left(x-1\right)>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =\dfrac{1}{2}\\\left[{}\begin{matrix}x>1\\x< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow x< 0\)
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x< 0\\x\ne-2\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}2x-1>=0\\x\left(x-1\right)< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{1}{2}\\0< x< 1\end{matrix}\right.\Leftrightarrow\dfrac{1}{2}< =x< 1\)