K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
1
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
13 tháng 2 2023
Bài 1:
Xét ΔBAK vuông tại A và ΔBHK vuông tại H có
BK chung
KA=KH
=>ΔBAK=ΔBHK
=>BA=BH
mà KA=KH
nên BK là trung trực của AH
=>BK vuông góc AH
QT
1
18 tháng 9 2023
Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:
\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
13 tháng 8
a: Ta có: \(\hat{AOD}+\hat{BOD}=180^0\) (hai góc kề bù)
=>\(\hat{BOD}=180^0-97^0=83^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\hat{AOE}<\hat{AOD}\left(56^0<97^0\right)\)
nên tia OE nằm giữa hai tia OA và OD
=>\(\hat{AOE}+\hat{EOD}=\hat{AOD}\)
=>\(\hat{EOD}=97^0-56^0=41^0\)
Ta có: \(\hat{AOE}+\hat{EOC}+\hat{COB}=180^0\)
=>\(\hat{EOC}=180^0-56^0-42^0=82^0\)
b: Trên cùng một nửa mặt phẳng bờ chứa tia OE, ta có; \(\hat{EOD}<\hat{EOC}\left(41^0<82^0\right)\)
nên tia OD nằm giữa hai tia OE và OC
=>\(\hat{EOD}+\hat{DOC}=\hat{EOC}\)
=>\(\hat{DOC}=82^0-41^0=41^0\)
Ta có: tia OD nằm giữa hai tia OE và OC
\(\hat{DOE}=\hat{DOC}\left(=41^0\right)\)
Do đó: OD là phân giác của góc EOC
KV
25 tháng 1 2024
\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)
AH
Akai Haruma
Giáo viên
31 tháng 1 2024
Lời giải:
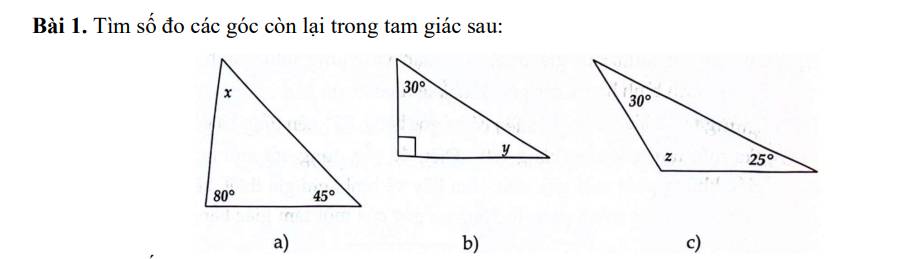
Áp dụng tính chất tổng 3 góc trong một tam giác bằng $180^0$
a.
$x=180^0-80^0-45^0=55^0$
b.
$y=180^0-30^0-90^0=60^0$
c.
$z=180^0-30^0-25^0=125^0$
f(1)=a+b+c+d=0
=>x=1 là nghiệm nếu a+b+c+d=0