Bài 1 : Chứng minh rằng một tứ giác lồi có 4 đỉnh cùng thuộc một cạch của tam giác đều cạnh bằng 2020cm thì không thể có 4 cạnh cùng lớn hơn 1010 cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 11 2018
Số phần tử của không gian mẫu là số cách chọn 4 đỉnh trong 32 đỉnh để tạo thành tứ giác, Ω = C 32 4
Gọi A là biến cố "chọn được hình chữ nhật".
Để chọn được hình chữ nhật cần chọn 2 trong 16 đường chéo đi qua tâm của đa giác, do đó số phần tử của A là C 16 2
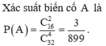
Chọn D
10 tháng 4 2016
a. Diện tích tam giác là :
6 x 6 = 36 ( cm2 )
chiều cao là :
36 x 2 : 15 = 4,8 ( cm )
b. Đáy bé là :
10 x 4/5 = 8 ( cm )
Chiều cao là :
10 : 100 x 60 = 6 ( cm )
Diện tích hình thang :
( 10 + 8 ) x 6 : 2 = 54 ( cm2 )
ĐS : ..........
Chúc bạn làm bài thi tốt !
TS
23 tháng 4 2023
Phát biểu a) là phát biểu sai. Vì một tam giác đều khi có ba cạnh bằng nhau không nhất thiết phải bằng 2cm, có thể bằng 3cm, 4cm, …
Phát biểu b) là đúng. Vì tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau.
Phát biểu c) là sai. Vì tam giác IKH chỉ có hai cạnh và hai góc bằng nhau nên chưa đủ điều kiện để tam giác IKH là tam giác đều.
DN
25 tháng 12 2017
Giả sử số tam giác là k
n=1 => k=1=12
n=2=> k=4=22
n=3=> k=9=32
...
n=2083=> k=20832=4338889
Vậy số tam giác được tạo thành là 4338889 tam giác