Cho tam giác ABC có góc BAC = 60o. Tia phân giác của góc ABC cắt AC tại E, tia phân giác của góc ACB cắt AB tại F. BE cắt CF tại I. Chứng minh IE = IF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 11 2018
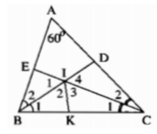
Trong ΔABC, ta có:
∠A +∠B +∠C = 180o (tổng ba góc trong tam giác)
⇒∠B +∠C = 180 - ∠A = 180 - 60 = 120o
+) Vì BD là tia phân giác của ABC nên: ∠(B1 ) = ∠(B2) = 1/2 ∠B
Vì CE là tia phân giác của góc ACB nên: ∠(C1 ) = ∠(C2) = 1/2 ∠ C
Do đó:
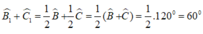
Trong ΔBIC, ta có:
∠(BIC) = 180o(∠(B1 ) + ∠(C1) = 180o - 60o = 120o
Kẻ tia phân giác ∠(BIC) cắt cạnh BC tại K
Suy ra: ∠(I2 ) = ∠(I3 ) = 1/2 ∠(BIC) = 60o
Ta có: ∠(I1 ) + ∠(BIC) = 180o (hai góc kề bù)
⇒ ∠(I1 ) = 180o-∠(BIC) = 180o - 120o = 60o
∠(I4 ) = ∠(I1) = 60o(vì hai góc đối đỉnh)
Xét ΔBIE và ΔBIK, ta có
∠(B2) = ∠(B1) (vì BD là tia phân giác của góc ABC)
BI cạnhchung
∠(I1) = ∠(I2) = 60o
Suy ra: ΔBIE = ΔBIK(g.c.g)
IK = IE (hai cạnh tương ứng) (1)
Xét ΔCIK và ΔCID, ta có
∠(C1) = ∠(C2) ( vì CE là tia phân giác của góc ACB).
CI cạnh chung
∠(I3) = ∠(I4) = 60o
Suy ra: ΔCIK = ΔCID(g.c.g)
IK = ID (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: IE = ID
16 tháng 4 2023
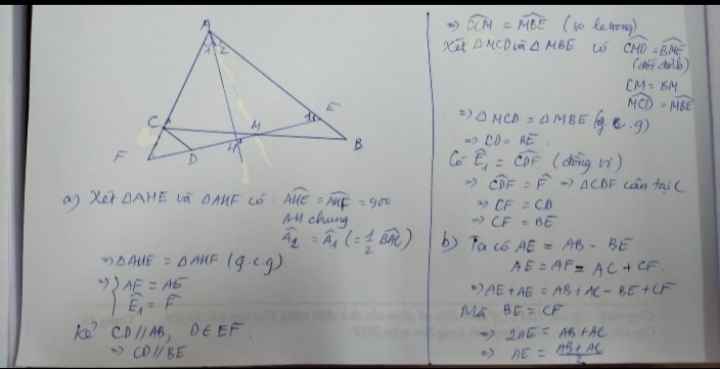
a: Sửa đề: góc ABD=góc AED
Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
=>DB=DE và góc ABD=góc AED
b: Xét ΔAEF vuông tại A và ΔABC vuông tại A có
AE=AB
góc AEF=góc ABC
=>ΔAEF=ΔABC
=>AF=AC
28 tháng 4 2023
a: AB<AC
=>góc B>góc C
góc ADB=góc DAC+góc ACD
góc ADC=góc BAD+góc ABD
mà góc ACD<góc ABD; góc BAD=góc CAD
nên góc ADB<góc ADC
b: Xét ΔABE có
AD vừa là đường cao, vừa là phân giác
=>ΔABE cân tại A
c: AD là phân giác
=>BD/AB=CD/AC
mà AB<AC
nên BD<CD
15 tháng 3 2016
Cho tam giác ABC :góc BAC =150 độ.Tia phân giác của góc B cắt AC tại E,tia phân giác góc C cắt AB tại F . Gọi I là giao điểm của BE và CF .Qua I vẽ đường thẳng vuông góc với IA ,cắt AB tại M và AC tại N .Hỏi :
a)Góc BIC =?
b)cmr:IM=TN=MN/2
c)cm:Góc MIB=góc ACB/2
Toán lớp 7
ai tích mình tích lại nha
6 tháng 8 2023
Sửa đề: ΔABC cân tại A
a:ΔABC cân tại A
mà AD là đường phân giác
nên AD là đường cao
=>AD vuông góc BC
b: Xét ΔAFI và ΔAEI có
AF=AE
góc FAI=góc EAI
AI chung
=>ΔAFI=ΔAEI
=>góc AFI=góc AEI
=>FI vuông góc AB
c: Xét ΔABC có
BE,AD là đường cao
BE cắt AD tại I
=>I là trực tâm
=>CI vuông góc AB
=>C,I,F thẳng hàng
Kẻ IH là phân giác của góc BIC
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{ABC}+\widehat{ACB}=180^0-60^0=120^0\)
=>\(2\cdot\left(\widehat{IBC}+\widehat{ICB}\right)=120^0\)
=>\(\widehat{IBC}+\widehat{ICB}=60^0\)
Xét ΔIBC có \(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^0\)
=>\(\widehat{BIC}+60^0=180^0\)
=>\(\widehat{BIC}=120^0\)
Ta có: \(\widehat{BIC}+\widehat{BIF}=180^0\)(hai góc kề bù)
=>\(\widehat{BIF}+120^0=180^0\)
=>\(\widehat{BIF}=60^0\)
Ta có: \(\widehat{BIF}=\widehat{EIC}\)(hai góc đối đỉnh)
mà \(\widehat{BIF}=60^0\)
nên \(\widehat{EIC}=60^0\)
IH là phân giác của góc BIC
=>\(\widehat{BIH}=\widehat{CIH}=\dfrac{\widehat{BIC}}{2}=60^0\)
Xét ΔFBI và ΔHBI có
\(\widehat{FBI}=\widehat{HBI}\)
BI chung
\(\widehat{FIB}=\widehat{HIB}\left(=60^0\right)\)
Do đó: ΔFBI=ΔHBI
=>IF=IH
Xét ΔIHC và ΔIEC có
\(\widehat{HIC}=\widehat{EIC}\)
IC chung
\(\widehat{HCI}=\widehat{ECI}\)
Do đó: ΔIHC=ΔIEC
=>IH=IE
mà IH=IF
nên IE=IF