3(2x-3)-9x=3-----giải bằng phương trình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 5 2021
\(\dfrac{x}{2x-6}-\dfrac{x}{2x+2}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\left(ĐKXĐ:x\ne-1,x\ne3\right)\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}-\dfrac{x}{2\left(x+1\right)}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)
\(\Leftrightarrow\dfrac{x\left(x+1\right)}{2\left(x+1\right)\left(x-3\right)}-\dfrac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{2x\cdot2}{2\left(x+1\right)\left(x-3\right)}\)
\(\Rightarrow x\left(x+1\right)-x\left(x-3\right)=4x\)
\(\Leftrightarrow x^2+x-x^2+3x=4x\)
\(\Leftrightarrow x^2+x-x^2+3x-4x=0\)
\(\Leftrightarrow0x=0\)
Phương trình có vô số nghiệm , trừ x = -1,x = 3
Vậy ...
\(\dfrac{12x+1}{12}< \dfrac{9x+1}{3}-\dfrac{8x+1}{4}\)
\(\Leftrightarrow12\cdot\dfrac{12x+1}{12}< 12\cdot\dfrac{9x+1}{3}-12\cdot\dfrac{8x+1}{4}\)
\(\Leftrightarrow12x+1< 4\left(9x+1\right)-3\left(8x+1\right)\)
\(\Leftrightarrow12x+1< 36x+4-24x-3\)
\(\Leftrightarrow12x+1< 12x+1\)
\(\Leftrightarrow12x-12x< 1-1\)
\(\Leftrightarrow0x< 0\)
Vậy S = {x | x \(\in R\)}
PT
2
CM
17 tháng 10 2018
Pt ⇔ 2 x + 3 + ( x + 2 ) ( 4 x + 1 ) = 2 x + 2 + 4 x + 1 . ĐK: x ≥ − 1 4
Đặt t 2 = 8 x + 4 ( x + 2 ) ( 4 x + 1 ) + 9 ⇔ 2 x + ( x + 2 ) ( 4 x + 1 ) = t 2 − 9 4
PTTT t 2 − 4 t + 3 = 0 ⇔ t = 1 hoặc t = 3
TH1. t = 1 giải ra vô nghiệm hoặc kết hợp với ĐK t ≥ 7 bị loại
TH 2 t = 3 ⇒ 2 x + 2 + 4 x + 1 = 3. Giải pt tìm được x = − 2 9 (TM)
Vậy pt có nghiệm duy nhất x = − 2 9
PT
2
HN
1
24 tháng 3 2020
-2x^5 - 7x^4 + 9x^3 = 0
<=> -x^3(2x^2 + 7x - 9) = 0
<=> -x^3(2x^2 + 9x - 2 - 9) = 0
<=> -x^3[x(2x + 9) - (2x + 9)] = 0
<=> x^3(x - 1)(2x + 9) = 0
<=> x^3 = 0 hoặc x - 1 = 0 hoặc 2x + 9 = 0
<=> x = 0 hoặc x = 1 hoặc x = -9/2
JP
0
28 tháng 4 2023
a: 3x-2=2x-3
=>x=-1
b: 2x+3=5x+9
=>-3x=6
=>x=-2
c: 5-2x=7
=>2x=-2
=>x=-2
d: 10x+3-5x=4x+12
=>5x+3=4x+12
=>x=9
e: 11x+42-2x=100-9x-22
=>9x+42=78-9x
=>18x=36
=>x=2
f: 2x-(3-5x)=4(x+3)
=>2x-3+5x=4x+12
=>7x-3=4x+12
=>3x=15
=>x=5
N
0
FF
0
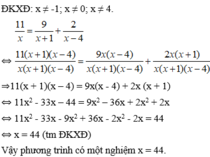
\(3\left(2x-3\right)-9x=3\)
\(\Leftrightarrow6x-9-9x=3\)
\(\Leftrightarrow-3x=12\)
\(\Leftrightarrow x=-4\)
Vậy x = -4