chứng tỏ rằng không tìm được hai số nguyên a,b thỏa mãn:
(a+b)(a-b)= -2022
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

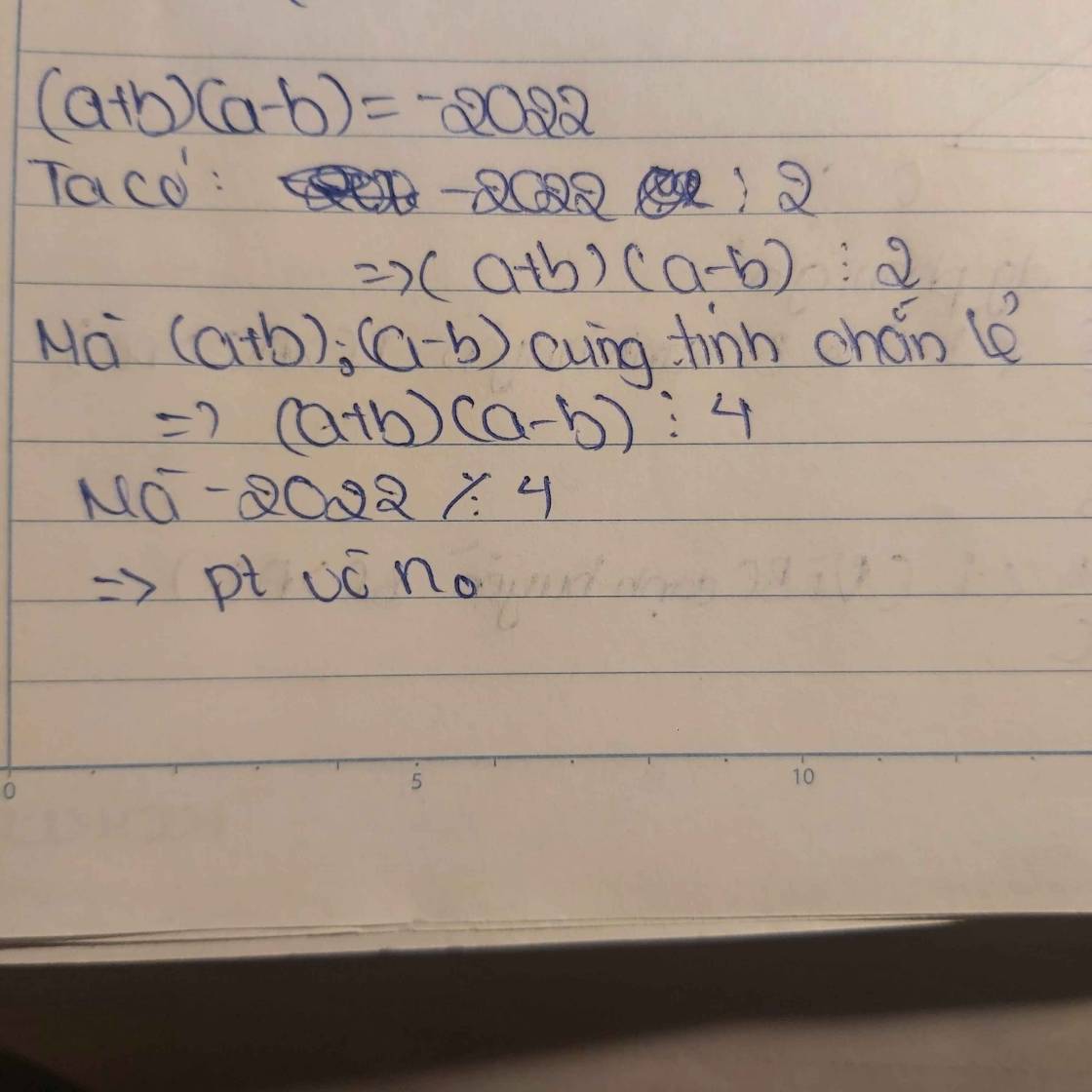


Ta có:
2a + 2021b = 2022a + b - a
Vậy phân số ban đầu có thể viết lại dưới dạng:
(2022a + b = a + 20206)/(3a + 2019b) -
= (2022a + b)/(3a + 2019b) + (20206
- a)/(3a + 2019b)
= 674 + (20206 - a)/(3a + 2019b)
Vì a, b là các số nguyên dương nên ta có:
0 < (20206 - a)/(3a + 2019b) < 1
Vậy phân số ban đầu không tối giản vì nó có thể viết dưới dạng tổng của một số nguyên và một phân số có tử số nhỏ hơn mẫu số.

1
\(M=\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}>\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}=1\)
\(M=\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}< \frac{a+c}{a+b+c}+\frac{b+a}{b+a+c}+\frac{c+b}{a+b+c}=2\)
=> M ko là số tự nhiên
2
\(a+b+c=0\)
\(\Rightarrow\left(a+b+c\right)^2=0\)
\(\Rightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=0\)
Do \(a^2+b^2+c^2\ge0\Rightarrow ab+bc+ca\le0\)
3
\(\left(x+y\right)\cdot35=\left(x-y\right)\cdot2010=xy\cdot12\)
\(\Rightarrow35x+35y=2010x-2010y\)
\(\Rightarrow35-2010x=2010y-35y\)
\(\Rightarrow-175x=-245y\)
\(\Rightarrow\frac{x}{y}=\frac{245}{175}=\frac{7}{5}\)
\(\Rightarrow\frac{x}{7}=\frac{y}{5}\)
Đặt \(\frac{x}{7}=\frac{y}{5}=k\)
\(\Rightarrow x=7k;y=5k\)
\(\Rightarrow\left(5k+7k\right)\cdot35=35k^2\cdot12\)
\(\Rightarrow k=k^2\Rightarrow k=1\left(k\ne0\right)\)
Vậy \(x=7;y=5\)
bài 2 chưa thuyết phục lắm, nếu \(a^2+b^2+c^2+2\left(ab+bc+ca\right)=0\) thì \(ab+bc+ca\ge0\) vẫn đúng, lẽ ra phải là \(ab+bc+ca=-\frac{\left(a^2+b^2+c^2\right)}{2}\le0\) *3*

a) Dễ thấy P = 102120 + 2120
= 102120 + 212.10
= 10(102119 + 212)
=> P \(⋮10\)
Lại có P = 102120 + 2120
= 10(102119 + 212)
= 10.(1000...00 + 212)
2119 số 0
= 10.1000...0212
2116 số 0
Tổng các chữ số của số S = 1000...0212 (2116 chữ số 0)
là 1 + 0 + 0 + 0 +.... + 0 + 2 + 1 + 2 (2116 hạng tử 0)
= 1 + 2 + 1 + 2 = 6 \(⋮3\)
=> S \(⋮3\Rightarrow P=10S⋮3\)
mà \(\left\{{}\begin{matrix}P⋮10\\P⋮3\\\left(10,3\right)=1\end{matrix}\right.\Rightarrow P⋮10.3\Rightarrow P⋮30\)
Gọi (a,b) = d \(\left(d\inℕ^∗;d\ne1\right)\)
=> \(\left\{{}\begin{matrix}a⋮d\\b⋮d\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2n+3⋮d\\5n+2⋮d\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}5.(2n+3)⋮d\\2.(5n+2)⋮d\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}10n+15⋮d\left(1\right)\\10n+4⋮d\left(2\right)\end{matrix}\right.\)
Lấy (1) trừ (2) ta được
(10n + 15) - (10n + 4) \(⋮d\)
<=> 11 \(⋮d\)
\(\Leftrightarrow d\in\left\{1;11\right\}\) mà d \(\ne1\)
<=> d = 11
Vậy (a;b) = 11

Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ bên trái khung soạn thảo) để được hỗ trợ tốt hơn.

Lời giải:
$a^3+b^3=(a+b)^3-3ab(a+b)=2013$
$\Rightarrow (a+b)^3=3ab(a+b)+2013\vdots 3$
$\Rightarrow a+b\vdots 3$
$\Rightarrow (a+b)^3\vdots 27$ và $3ab(a+b)\vdots 9$
Do đó:
$2013=(a+b)^3-3ab(a+b)\vdots 9$
Điều này vô lý do $2013\not\vdots 9$
Vậy không tồn tại $a,b$ nguyên thỏa mãn đề.