Chi tiết nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 8 2023
5:
a: \(-120x^5y^4=20x^5y^2\cdot\left(-6y^2\right)\)
b: \(60x^6y^2=20x^5y^2\cdot3x\)
c: \(-5x^{15}y^3=20x^5y^2\cdot\left(-\dfrac{1}{4}x^{10}y\right)\)
d: \(2x^{12}y^{10}=20x^5y^2\cdot\left(\dfrac{1}{10}x^7y^8\right)\)
GN
GV Ngữ Văn
Giáo viên
17 tháng 12 2018
* Ý nghĩa chi tiết tiếng đàn
- Tiếng đàn vừa thể hiện tài năng, vừa nói lên nỗi lòng của Thạch Sanh khi bị giam trong ngục.
- Tiếng đàn cũng giúp công chúa khỏi bị câm, giúp Thạch Sanh giải được nỗi oan uổng.
- Tiếng đàn còn có giá trị biểu tượng, giống như tiếng đàn của vua Nghiêu vua Thuấn trong điển tích. Tiếng đàn là ước mơ của nhân dân tự ngàn đời về một đất nước thái bình thịnh trị. Tiếng đàn Thạch Sanh có sức mạnh cảm hóa quân thù, đẩy lùi được cuộc binh đao, tránh hi sinh xương máu của nhân dân vào cuộc chiến tranh phi nghĩa.
* Chi tiết niêu cơm thần có ý nghĩa:
- Niêu cơm bé tí nhưng ăn mãi lại đầy khiến cả 18 nước chư hầu đều thán phục và bỏ giáp xin hàng.
- Niêu cơm là ước mơ của nhân dân về cuộc sống no ấm, đủ đầy, đất nước không đói nghèo, loạn lạc.
NT
1
Z
11 tháng 2 2022
refer
Chi tiết tiêu biểu là hình ảnh đám tang của dế , qua đó cho thấy sự cảm thông và hối hạn các bạn
HT
2
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1
\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)
T
12 tháng 1
d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)
Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)
10 tháng 3 2017
Chú tư làm 2 chi tiết hết số thời gian là
2 giờ 15 phút + 1 giờ 40 phút=3 giờ 55 phút
Chú tư làm chi tiêt thứ 3 trong số giờ là
6 giờ 30 phút - 3 giờ 55 phút =2 giờ 35 phút
2
7 tháng 5 2021
Ta có tổng số chi tiết máy lắp được là 200.
- Người thứ nhất lắp được 1/4 tổng số chi tiết máy, tức là:
200 . 1/4 = 50 (chi tiết máy)
- Người thứ hai lắp được 0,4 tổng số chi tiết máy, tức là:
200 . 0,4 = 80 (chi tiết máy)
- Người thứ ba lắp được 50% so với người thứ hai, tức là:
80 . 50% = 80 . 0,5 = 40 (chi tiết máy)
- Vậy người thứ tư lắp được là tổng số máy trừ đi 3 người đầu, tức số máy của người thứ tư là:
200 - (50 + 80 + 40) = 30 (chi tiết máy).
Đáp số: 30 chi tiết máy.
T
10 tháng 6 2021
Gọi x, y lần lượt là số chi tiết máy mà 2 tổ sản xuất được trong tháng thứ nhất (0 < x, y < 900; x, y ∈ N)
Vì tháng thứ nhất hai tổ sản xuất được 900 chi tiết máy
=> x+y=900 (1)
Vì tháng thứ 2 tổ I vượt mức 15% và tổ II vượt mức 10%so với tháng thứ nhất, vì vậy hai tổ sản xuất được 1010 chi tiết máy
=> (x+15%x)+(y+10%y)=1010
<=> 1,15x+1,1y=1010
Từ (1),(2) ta có hệ:
\(\left\{{}\begin{matrix}x+y=900\\1,15x+1,1y=1010\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=400\\y=500\end{matrix}\right.\left(tm\right)}\)
Vậy ....
10 tháng 3 2016
chi tiết máy thứ 3 làm hết số thời gian là :
5 giờ 30 phút-1 giờ 30 phút-1 giờ 40 phút=2 giờ 20 phút
tích ĐÚNG chị nha em
10 tháng 3 2016
Thời gian để làm chi tiết máy thứ ba là :
5 giờ 30 phút - 1 giờ 30 phút - 1 giờ 40 phút = 2 giờ 20 phút
Đáp số : 2 giờ 20 phút
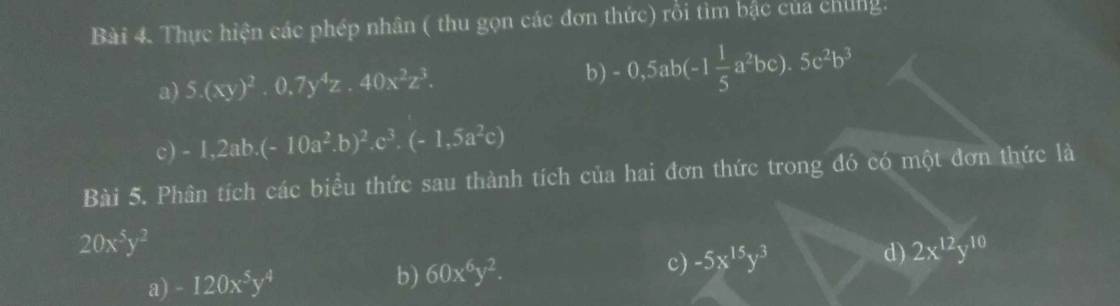
\(N=\left(\dfrac{3x}{2x-2}-\dfrac{3x}{2x+2}-\dfrac{3x-2}{x^2-1}\right)\cdot\dfrac{4x^2-4}{3}\left(x\ne\pm1\right)\)
\(=\left[\dfrac{3x}{2\left(x-1\right)}-\dfrac{3x}{2\left(x+1\right)}-\dfrac{3x-2}{\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{4x^2-4}{3}\)
\(=\left[\dfrac{3x\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}-\dfrac{3x\left(x-1\right)}{2\left(x-1\right)\left(x+1\right)}-\dfrac{2\cdot\left(3x-2\right)}{2\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{3}\)
\(=\dfrac{3x^2+3x-3x^2+3x-6x+4}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4\left(x-1\right)\left(x+1\right)}{3}\)
\(=\dfrac{4\cdot2}{3}\)
\(=\dfrac{8}{3}\)
Vậy giá trị của \(N\) không phụ thuộc vào biến \(x\).
\(N=\left(\dfrac{3x}{2x-2}-\dfrac{3x}{2x+2}-\dfrac{3x-2}{x^2-1}\right)\cdot\dfrac{4x^2-4}{3}\\ =\left(\dfrac{3x}{2\left(x-1\right)}-\dfrac{3x}{2\left(x+1\right)}-\dfrac{3x-2}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{4x^2-4}{3}\\ =\dfrac{3x\left(x+1\right)-3x\left(x-1\right)-2\left(3x-2\right)}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4x^2-4}{3}\\ =\dfrac{\left(3x^2+3x\right)-\left(3x^2-3x\right)-\left(6x-4\right)}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4x^2-4}{3}\)
\(=\dfrac{3x^2+3x-3x^2+3x-6x+4}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4\left(x-1\right)\left(x+1\right)}{3}\\ =\dfrac{4}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4\left(x-1\right)\left(x+1\right)}{3}\\ =\dfrac{4\cdot2}{3}\)
`=8/3`
`->N` không phụ thuộc vào biến `x`
`color{blue}{ @ A_ri}`