Mẫu số chung của các phân số này là bao nhiêu?
\(\dfrac{3}{10}\);\(\dfrac{-3}{4}\);\(\dfrac{-5}{6}\);\(\dfrac{7}{15}\);\(0\);\(\dfrac{2}{5}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{1}{440}+\frac{3}{440}+\frac{6}{440}+...+\frac{45}{440}\)
\(=\frac{1}{440}+\frac{1+2}{440}+\frac{3+3}{440}+\frac{6+4}{440}+...+\frac{35+10}{440}\)
\(=\frac{1+3+6+10+15+21+28+36+45}{440}\)
\(=\frac{165}{440}=\frac{3}{8}\)

có các phân số là:
6/10; 10/6;5/12;12/5;15/4;4/15;3/20;20/3;30/2;2/30;1/60;60/1
Cho nên có 12 phân số

Vì các phân số đều có mẫu số giống nhau nên chỉ cần tính tử số.
Các tử số có quy luật là :
1 + 2 = 3
3 + 3 = 6
6 + 4 = 10
Vậy các số đó là :
1, 3, 6, 10, 15, 21, 28, 36, 45
Tổng của các số trên là :
1 + 3 + 6 + ... + 45 = 165
Vậy tổng là \(\frac{165}{440}=\frac{3}{8}\)

Đề trước mình giải rõ ra rồi giờ mình cộng thêm vào :
\(\frac{165+55}{440}=\frac{1}{2}\)

Gọi phân số tối giản phải tìm là a/b; (a; b ∈ Z; b ≠ 1), ƯCLN (a, b) = 1
Ta có a.b = 3150 = 2. 32. 52. 7 và a, b đều là ước của 3150.
Vì phân số này có thể viết được dưới dạng số thập phân hữu hạn nên b chỉ có ước nguyên tố là 2 và 5.
Do đó, b ∈ {2; 25; 50}.
- Với b = 2 thì a = 3150:2 = 1575
- Với b = 25 thì a = 3150:25 = 126
- Với b = 50 thì a = 3150:50 = 63
Vậy các phân số phải tìm là:
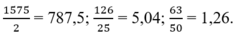
Ta có:
\(10=2\cdot5\)
\(4=2^2\)
\(6=2\cdot3\)
\(15=3\cdot5\)
\(0=0\)
\(5=5\)
\(\Rightarrow BCNN\Rightarrow MC\left(10;4;6;15;0;5\right)=2^2\cdot3\cdot5=60\)
\(\Rightarrow MC\) của các phân số trên là \(60.\)
Mẫu số chung: 60