choΔabc ọn (ab<ac) gọi m là trung điểm của bc.trên tia am lấy điểm m sao cho m là trung điểm của an
a)cmr:Δamb=Δnmc
b) vẽ cd vuông góc ab (dϵab)so sánh góc abc và góc bcn.tính góc dcn
vẽ hình nhé❤
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có: AM=MD (gt)
MC=MB(gt)
\(\widehat{AMC}=\widehat{BMD}\)( góc đối tạo bởi hai đường thẳng)
=> \(\Delta AMC=\Delta DMB\)(1)
b, (1) => AC=BD
c, Ta có: góc MAC= góc MBD ( ΔAMC=ΔDMB)
=> AC// BD
mà AC vuông góc AB => BD vuông góc AC

Dựng hình bình hành ABDC \(\Rightarrow\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\)
\(\left|\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{MA}\right|=\left|\overrightarrow{MC}+\overrightarrow{BA}+\overrightarrow{CB}\right|\)
\(\Leftrightarrow\left|\overrightarrow{AD}+\overrightarrow{MA}\right|=\left|\overrightarrow{MC}+\overrightarrow{CA}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MD}\right|=\left|\overrightarrow{MA}\right|\)
\(\Leftrightarrow MD=MA\)
\(\Rightarrow\) Tập hợp M là đường trung trực của đoạn thẳng AD

a; Xét ΔABC co AM/AB=AN/AC
nên MN//BC
=>ΔAMN đồng dạng với ΔBAC
=>\(\dfrac{S_{AMN}}{S_{ABC}}=\left(\dfrac{AM}{AB}\right)^2=\dfrac{1}{4}\)
=>\(S_{AMN}=30\left(cm^2\right)\)
b: MN/BC=AM/AB=1/2

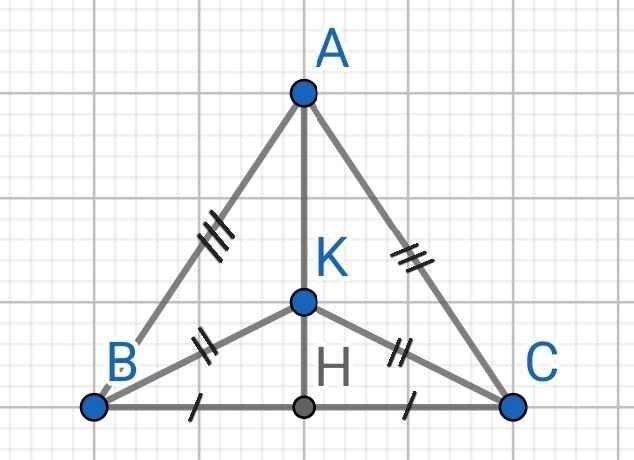
∆ABC cân tại A
⇒ H là trung điểm BC
⇒ AH là đường trung trực của ABC
⇒ AH là đường trung trực của BC
Ta có:
KB = KC (gt)
⇒ K nằm trên đường trung trực của BC
Mà AH là đường trung trực của BC
⇒ K ∈ AH
⇒ A, K, H thẳng hàng

\(\dfrac{18}{30}=\dfrac{18:3}{30:3}=\dfrac{6}{10}=\dfrac{6:2}{10:2}=\dfrac{3}{5}\)

a: Ta có: H và D đối xứng với nhau qua AB
nên AH=AD; BH=BD
=>ΔAHD cân tại A
=>AB là tia phân giác của góc HAD(1)
Ta có: H và E đối xứng với nhau qua AC
nên AH=AE; CH=CE
=>ΔAHE cân tại A
=>AC là tia phân giác của góc HAE(2)
Từ (1) và (2) suy ra \(\widehat{EAD}=2\cdot\left(\widehat{BAH}+\widehat{CAH}\right)=2\cdot90^0=180^0\)
=>E,A,D thẳng hàng
mà AD=AE(=AH)
nên A là trung điểm của ED
b: Xét ΔDHE có
HA là đường trung tuyến
HA=DE/2
DO đó: ΔDEH vuông tại H
c: Xét ΔAHB và ΔADB có
AH=AD
HB=DB
AB chung
Do đó: ΔAHB=ΔADB
Suy ra: \(\widehat{AHB}=\widehat{ADB}=90^0\)
Xét ΔCHA và ΔCEA có
CH=CE
HA=EA
CA chung
DO đó: ΔCHA=ΔCEA
Suy ra: \(\widehat{CHA}=\widehat{CEA}=90^0\)
Xét tứ giác BDEC có BD//CE
nên BDEC là hình thang
mà \(\widehat{BDE}=90^0\)
nên BDEC là hình thang vuông
A B C M N D
a/ Xét tg AMB và tg NMC có
MB=MC (gt)
MA=MN (gt)
\(\widehat{AMB}=\widehat{NMC}\) (góc đối đỉnh)
=> tg AMB = tg NMC (c.g.c)
b/
Ta có
tg AMB = tg NMC (cmt) \(\Rightarrow\widehat{ABC}=\widehat{BCN}\) Hai góc trên ở vị trí sole trong
=> AB//CN
\(\Rightarrow\widehat{ADC}=\widehat{DCN}\) (góc so le trong) mà \(\widehat{ADC}=90^o\)
\(\Rightarrow\widehat{DCN}=90^o\)