Hai đường thẳng xy và x'y' cắt nhau tại O. Gọi OM và AON theo thứ tự là tia phân giác của góc xOx' và yOy'. Hai tia OM và On có phải là hai tia đối nhau không? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


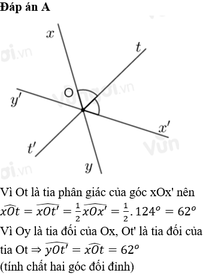
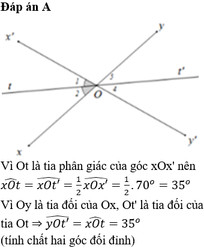
Ta có hình vẽ:
\(\widehat{xOx'}\) và \(\widehat{yOy'}\) đối đỉnh.
\(\Rightarrow\widehat{xOx'}=\widehat{yOy'}\)
\(Om\) là tia phân giác của \(\widehat{xOx'}\) nên: \(\widehat{mOx}=\widehat{mOx'}=\dfrac{1}{2}\widehat{xOx'}\)
\(On\) là tia phân giác của \(\widehat{yOy'}\) nên \(\widehat{mOy}=\widehat{mOy'}=\dfrac{1}{2}\widehat{yOy'}\)
Mà:
\(\widehat{mOy}\) và \(\widehat{mOx}\) kề bù nên:
\(\widehat{mOy}+\widehat{mOx}=\widehat{mOn}=180^o\)
Vậy \(Om\) đối \(On\)

a) Góc yOm = 1800 - 1000 = 800
Góc yOn = 1800 - 300 = 1500 . => góc yOm < góc yOn => đpcm
b) Góc mOn = góc yOn - góc yOm = 1500 - 800 = 700
c) góc yOt = góc yOm = 800
d) góc aOm = 1/2 góc yOm = 400
góc mOn = 700 => góc aOn = góc aOm + góc mOn = 700 + 400 =1100
mik ko chắc là đúng ko
nhưng các bn ui
tk cho mik vài cái
nha nha
Thanks bạn, mik đã k đúng cho bạn ! ^_^