Mình dg cần rất gấp luon ạ mog mn giúp đỡ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Trong câu ghép : " Đôi mắt khuyên vòng trắng long lanh, đôi chân thanh thoát "
→ Có 2 vế câu
→ Các vế câu được nối bằng dấu " , "


Câu 8:
a. Với $x,y$ là số nguyên thì $x, y-3$ cũng là số nguyên. Mà $x(y-3)=15$ nên ta có các TH:
TH1: $x=1, y-3=15\Rightarrow x=1; y=18$ (tm)
TH2: $x=-1, y-3=-15\Rightarrow x=-1; y=-12$ (tm)
TH3: $x=15; y-3=1\Rightarrow x=15; y=4$ (tm)
TH4: $x=-15; y-3=-1\Rightarrow x=-15; y=2$ (tm)
TH5: $x=3, y-3=5\Rightarrow x=3; y=8$ (tm)
TH6: $x=-3; y-3=-5\Rightarrow x=-3; y=-2$ (tm)
TH7: $x=5; y-3=3\Rightarrow x=5; y=6$ (tm)
TH8: $x=-5; y-3=-3\Rightarrow x=-5; y=0$ (tm)
Câu 8:
b.
$xy-2y+3(x-2)=7$
$\Rightarrow y(x-2)+3(x-2)=7$
$\Rightarrow (x-2)(y+3)=7$
Do $x,y$ nguyên nên $x-2, y+3$ nguyên. Mà tích của chúng bằng $7$ nên ta có các TH sau:
TH1: $x-2=1, y+3=7\Rightarrow x=3; y=4$ (tm)
TH2: $x-2=-1; y+3=-7\Rightarrow x=1; y=-10$ (tm)
TH3: $x-2=7, y+3=1\Rightarrow x=9; y=-2$ (tm)
TH4: $x-2=-7; y+3=-1\Rightarrow x=-5; y=-4$ (tm)


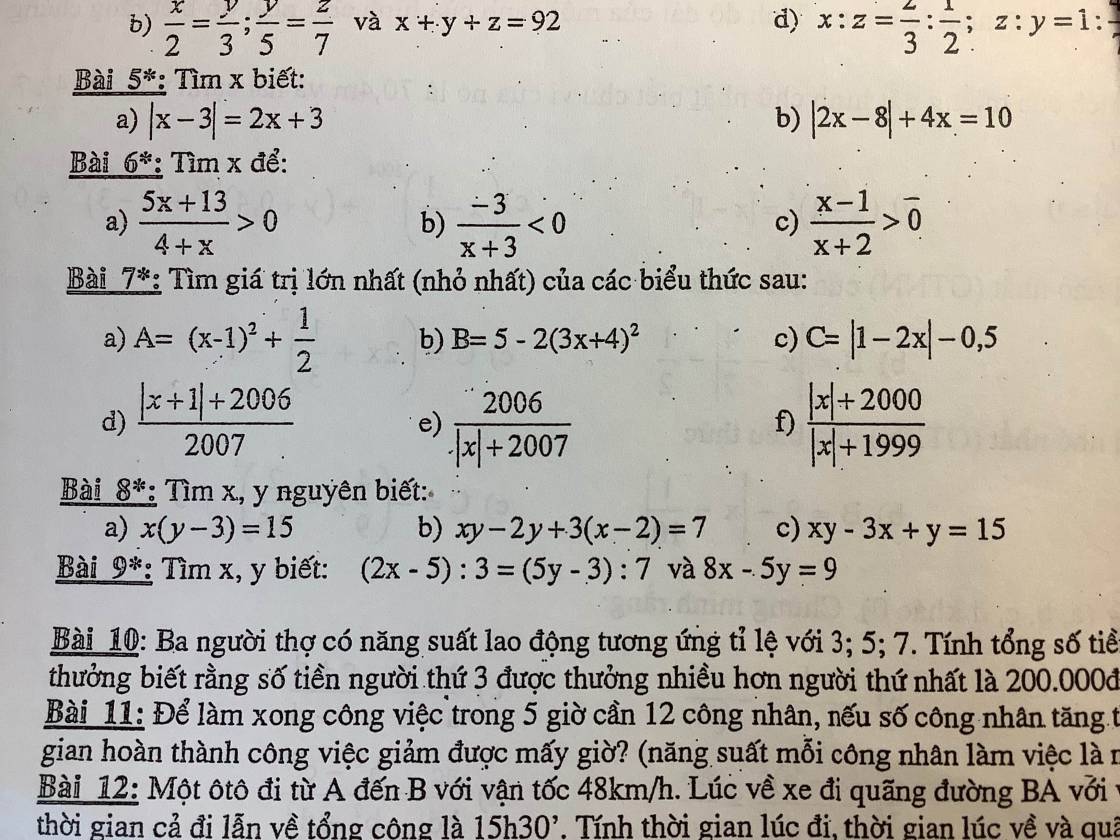
Bài 5:
Thay x=1 và y=2 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}-m\cdot1+2=-2m\\1+m^2\cdot2=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2m=-m+2\\2m^2=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\-m=2\end{matrix}\right.\)
=>m=-2
Bài 6:
a: ĐKXĐ: x>=1 và y>=-2
\(\left\{{}\begin{matrix}\sqrt{x-1}-3\sqrt{y+2}=2\\2\sqrt{x-1}+5\sqrt{y+2}=15\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2\sqrt{x-1}-6\sqrt{y+2}=4\\2\sqrt{x-1}+5\sqrt{y+2}=15\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-11\sqrt{y+2}=-11\\\sqrt{x-1}-3\sqrt{y+2}=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{y+2}=1\\\sqrt{x-1}=2+3=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y+2=1\\x-1=25\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=26\\y=-1\end{matrix}\right.\left(nhận\right)\)
b: ĐKXĐ: x<>0 và y<>0
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{8}{x}+\dfrac{15}{y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8}{x}+\dfrac{8}{y}=\dfrac{8}{12}=\dfrac{2}{3}\\\dfrac{8}{x}+\dfrac{15}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{7}{y}=\dfrac{-1}{3}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=21\\\dfrac{1}{x}=\dfrac{1}{12}-\dfrac{1}{21}=\dfrac{7-4}{84}=\dfrac{3}{84}=\dfrac{1}{28}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=28\\y=21\end{matrix}\right.\left(nhận\right)\)
c: ĐKXĐ: x<>0 và y<>2
\(\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{3}{y-2}=4\\\dfrac{4}{x}-\dfrac{1}{y-2}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{6}{y-2}=8\\\dfrac{4}{x}-\dfrac{1}{y-2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{y-2}=7\\\dfrac{2}{x}+\dfrac{3}{y-2}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y-2=1\\\dfrac{2}{x}=4-\dfrac{3}{1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\left(nhận\right)\)
d: ĐKXĐ: x<>-2y và x<>-y/2
\(\left\{{}\begin{matrix}\dfrac{2}{x+2y}+\dfrac{1}{2x+y}=3\\\dfrac{4}{x+2y}-\dfrac{3}{2x+y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{6}{x+2y}+\dfrac{3}{2x+y}=9\\\dfrac{4}{x+2y}-\dfrac{3}{2x+y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{x+2y}=10\\\dfrac{4}{x+2y}-\dfrac{3}{2x+y}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+2y=1\\\dfrac{3}{2x+y}=4-1=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2y=1\\2x+y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=2\\2x+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3y=1\\x+2y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=1-\dfrac{2}{3}=\dfrac{1}{3}\end{matrix}\right.\left(nhận\right)\)
e: ĐKXĐ: x>4 và y<>-2
\(\left\{{}\begin{matrix}\dfrac{3}{\sqrt{x-4}}+\dfrac{4}{y+2}=7\\\dfrac{5}{\sqrt{x-4}}-\dfrac{1}{y+2}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{3}{\sqrt{x-4}}+\dfrac{4}{y+2}=7\\\dfrac{20}{\sqrt{x-4}}-\dfrac{4}{y+2}=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{23}{\sqrt{x-4}}=23\\\dfrac{5}{\sqrt{x-4}}-\dfrac{1}{y+2}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x-4}=1\\\dfrac{1}{y+2}=5-4=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-4=1\\y+2=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\left(nhận\right)\)
f: ĐKXĐ: x>=-1
\(\left\{{}\begin{matrix}2\left(x+y\right)+\sqrt{x+1}=4\\\left(x+y\right)-\sqrt{x+1}=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2\left(x+y\right)+\sqrt{x+1}+\left(x+y\right)-\sqrt{x+1}=4-5=-1\\\left(x+y\right)-\sqrt{x+1}=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3\left(x+y\right)=-1\\\sqrt{x+1}=-\dfrac{1}{3}+5=\dfrac{14}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+y=-\dfrac{1}{3}\\x+1=\dfrac{196}{9}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{187}{9}\\y=-\dfrac{1}{3}-\dfrac{187}{9}=-\dfrac{190}{9}\end{matrix}\right.\left(nhận\right)\)
Nhiều quá em, em chỉ nên đăng những câu nào cảm thấy khó khăn khi giải quyết thôi