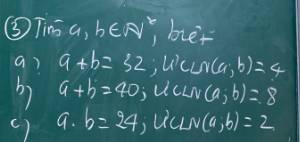
cần giúp gấp bài này ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


lần đổ 1
\(\left(mC+m'C'\right).\left(38-20\right)=mC.\left(60-38\right)\)
\(\Leftrightarrow\left(mC+m'C'\right)18=mC.22\)
\(\Leftrightarrow2mC=9m'C'\)
lần 2 \(\left(2mC+m'C'\right)\left(t_x-38\right)=mC.\left(60-t_x\right)\)
\(11m'C'\left(t_x-38\right)=\dfrac{9}{2}.m'C'\left(60-t_x\right)\)
\(\Rightarrow t_x=...\)

Bài 6:
a: Xét tứ giác DEBF có
DE//BF
DE=BF
Do đó: DEBF là hình bình hành




a: Xét tứ giác MBQC có
N la trung điểm chung của MQ và BC
=>MBQC là hình bình hành
b: Xet tứ giácc AMQC có
AM//QC
AM=QC
góc MAC=90 độ
=>AMQC là hình chữ nhật
c: Xét ΔBAC có
N là trung điểm của CB
NK//AB
=>K là trung điểm của AC
Xét ΔCAB có
AN,BK,CM là các trung tuyến
nên ba đường này sẽ đồng quy
=>B,H,K thẳng hàng

\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)

a: ƯCLN(a,b)=4
=>\(\left\{{}\begin{matrix}a=4x\\b=4y\end{matrix}\right.\left(x,y\in Z^+\right)\)
a+b=32
=>4x+4y=32
=>x+y=8
mà x,y là các số nguyên dương
nên \(\left(x,y\right)\in\left\{\left(1;7\right);\left(2;6\right);\left(3;5\right);\left(4;4\right);\left(5;3\right);\left(6;2\right);\left(7;1\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(4;28\right);\left(8;24\right);\left(12;20\right);\left(16;16\right);\left(20;12\right);\left(24;8\right);\left(28;4\right)\right\}\)
mà ƯCLN(a,b)=4
nên \(\left(a,b\right)\in\left\{\left(4;28\right);\left(12;20\right);\left(20;12\right);\left(28;4\right)\right\}\)
b: ƯCLN(a,b)=8
=>\(\left\{{}\begin{matrix}a=8c\\b=8d\end{matrix}\right.\left(c,d\in Z^+\right)\)
a+b=40
=>8c+8d=40
=>8(c+d)=40
=>c+d=5
mà c,d là các số nguyên dương
nên \(\left(c,d\right)\in\left\{\left(1;4\right);\left(4;1\right);\left(2;3\right);\left(3;2\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(8;32\right);\left(32;8\right);\left(16;24\right);\left(24;16\right)\right\}\)
c: ƯCLN(a,b)=2
=>\(\left\{{}\begin{matrix}a=2e\\b=2f\end{matrix}\right.\left(e,f\in Z^+\right)\)
a*b=24
=>\(2\cdot e\cdot2\cdot f=24\)
=>\(4\cdot e\cdot f=24\)
=>\(e\cdot f=6\)
mà e,f là các số nguyên dương
nên \(\left(e,f\right)\in\left\{\left(1;6\right);\left(2;3\right);\left(3;2\right);\left(6;1\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(2;12\right);\left(4;6\right);\left(6;4\right);\left(12;2\right)\right\}\)
ƯCLN (a,b) = 8
a = 8x
b = 8y
Mà a + b = 32
Nên 8x + 8y = 32
8(x + y) = 32
x + y = 32 : 8
x + y = 4
Do đó, ta có bảng sau :
Vậy a ; b = 0 ; 32
a ; b = 8 ; 24
a ; b = 16 ; 16
a ; b = 24 ; 8
a ; b = 32 ; 0
em thấy trên web khác có bạn làm thế này í ah (nếu ƯCLN(a,b)=8