Trong mặt phẳng tọa độ cho 2 đường thẳng mx-y=2 (1) và (2-m)x+y=m (2).Tìm m để giao điểm A của 2 đường thẳng (1) và (2) thỏa mãn góc BAC=900 .Tính diện tích tam giác ABC ứng với m tìm được
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 3 2022
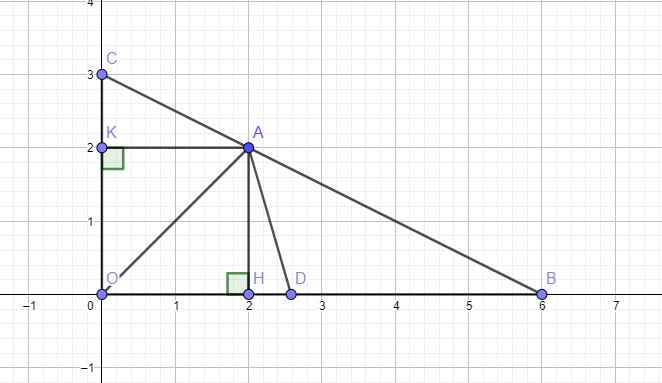
Gọi pt BC có dạng: \(y=ax+b\Rightarrow\left\{{}\begin{matrix}0=6a+b\\3=a.0+b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=3\\a=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow y=-\dfrac{1}{2}x+3\)
Pt hoành độ giao điểm BC và d:
\(-\dfrac{1}{2}x+3=mx-2m+2\)
\(\Leftrightarrow m\left(x-2\right)+\dfrac{1}{2}\left(x-2\right)=0\)
\(\Leftrightarrow\left(m+\dfrac{1}{2}\right)\left(x-2\right)=0\Rightarrow x=2\Rightarrow y=2\)
Vậy \(d_m\) luôn cắt BC tại điểm A cố định có tọa độ \(A\left(2;2\right)\)
b. Ta có: \(OB=\left|x_B\right|=6;OC=\left|y_C\right|=3\)
Từ A kẻ AH vuông góc trục hoành và AK vuông góc trục tung
\(\Rightarrow AH=\left|y_A\right|=2\) ; \(AK=\left|x_A\right|=2\)
\(S_{OAC}=\dfrac{1}{2}AK.OC=\dfrac{1}{2}.2.3=3\) ; \(S_{OAB}=\dfrac{1}{2}AH.OB=6\)
\(S_{OBC}=\dfrac{1}{2}OB.OC=9\)
Giả sử \(d_m\) cắt cạnh OC tại 1 điểm D nằm giữa O và C
\(\Rightarrow S_{ACD}=S_{OAC}-S_{OAD}< S_{OAC}=3< \dfrac{1}{2}S_{OBC}=9\) (ktm)
\(\Rightarrow d_m\) phải cắt cạnh OB tại 1 điểm D nào đó nằm giữa O và B
Khi đó: \(S_{ABD}=\dfrac{1}{2}S_{OBC}=\dfrac{9}{2}\)
Mà \(S_{ABD}=\dfrac{1}{2}AH.BD\Rightarrow BD=\dfrac{2S_{ABD}}{AH}=\dfrac{9}{2}\)
\(\Rightarrow x_B-x_D=\dfrac{9}{2}\Rightarrow x_D=6-\dfrac{9}{2}=\dfrac{3}{2}\)
\(\Rightarrow D\left(\dfrac{3}{2};0\right)\)
Do \(d_m\) qua D nên: \(\dfrac{3}{2}m-2m+2=0\Rightarrow m=4\)
27 tháng 1
b: Thay m=2 vào (d), ta được:
y=2x-2+1=2x-1
Phương trình hoành độ giao điểm là:
\(x^2=2x-1\)
=>\(x^2-2x+1=0\)
=>(x-1)^2=0
=>x-1=0
=>x=1
Thay x=1 vào (P), ta được:
\(y=1^2=1\)
Vậy: Khi m=2 thì (P) cắt (d) tại A(1;1)
b: Phương trình hoành độ giao điểm là:
\(x^2=2x-m+1\)
=>\(x^2-2x+m-1=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot1\cdot\left(m-1\right)\)
=4-4m+4
=-4m+8
Để (P) cắt (d) tại hai điểm phân biệt thì Δ>0
=>-4m+8>0
=>-4m>-8
=>m<2
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\\x_1x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)
y1,y2 thỏa mãn gì vậy bạn?
3 tháng 4 2023
a: Khi m=-1 thì (d): y=-x+1-(-1)=-x+2
PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1
b: PTHĐGĐ là:
x^2-mx+m-1=0
Δ=(-m)^2-4(m-1)
=m^2-4m+4=(m-2)^2>=0
Để (P) cắt (d) tại hai điểm pb thì m-2<>0
=>m<>2
\(\sqrt{x_1}+\sqrt{x_2}=3\)
=>x1+x2+2 căn x1x2=9
=>\(m+2\sqrt{m-1}=9\)
=>\(m-1+2\sqrt{m-1}=8\)
=>\(\left(\sqrt{m-1}+4\right)\left(\sqrt{m-1}-2\right)=0\)
=>m=5
13 tháng 11 2021
Giải thích các bước giải:
a,Thay m=3m=3 vào (d)(d) ta đc: y=2x−3y=2x-3
có đường thẳng (d)(d) đi qua điểm B(0;−3)B(0;-3) và điểm A(32;0)A(32;0)
Có tam giác tạo bởi (d)(d) và 2 trục tọa độ là ΔOABΔOAB
Có OA=∣∣∣32∣∣∣=32;OB=|−3|=3OA=|32|=32;OB=|-3|=3
→SOAB=12.OA.OB=12.3/2.3=94(đvdt)→SOAB=12.OA.OB=12.3/2.3=94(đvdt)
Vậy SOAB=94đvdtSOAB=94đvdt
b,Để (d)(d) cắt đt y=−x+1y=-x+1 ⇔m−1≠−1⇔m-1≠-1
⇔m≠0⇔m≠0
Để (d) cắt đt y=−x+1y=-x+1 tại điểm có hoành độ bằng −2-2
Thay x=−2x=-2 vào 2 công thức hàm số ta đc hpt:
{y=(m−1).(−2)−my=2+1=3{y=(m−1).(−2)−my=2+1=3
→{3=−2m+2−my=3{3=−2m+2−my=3
↔{−3m=1y=3{−3m=1y=3
↔{m=−13y=3{m=−13y=3
→m=−13→m=-13(thỏa mãn)
Vậy m=−13m=-13
14 tháng 5 2021
a) Khi m = 2 thì: \(\hept{\begin{cases}y=x^2\\y=2x+3\end{cases}}\)
Hoành độ giao điểm (P) và (d) là nghiệm của PT: \(x^2=2x+3\Leftrightarrow x^2-2x-3=0\Leftrightarrow\left(x+1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x-3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1\Rightarrow y=1\\x=3\Rightarrow y=9\end{cases}}\)
Vậy tọa độ giao điểm của (P) và (d) là \(\left(-1;1\right)\) và \(\left(3;9\right)\)
b) Hoành độ giao điểm của (P) và (d) là nghiệm của PT:
\(x^2=mx+3\Leftrightarrow x^2-mx-3=0\)
Vì \(ac=1\cdot\left(-3\right)< 0\) => PT luôn có 2 nghiệm phân biệt
Theo hệ thức viet ta có: \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=-3\end{cases}}\)
Mà \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{3}{2}\Leftrightarrow\frac{x_1+x_2}{x_1x_2}=\frac{3}{2}\Leftrightarrow\frac{-m}{3}=\frac{3}{2}\Rightarrow m=-\frac{9}{2}\)
Vậy \(m=-\frac{9}{2}\)
10 tháng 4 2022
a) Lập phương trình hoành độ giao điểm:
x2 = mx + 3
<=> x2 - mx - 3 = 0
Tọa độ (P) và (d) khi m = 2:
<=> x2 - 2x - 3 = 0
<=> \(\orbr{\begin{cases}x_1=3\\x_2=-1\end{cases}}\) => \(\orbr{\begin{cases}y_1=9\\y_2=1\end{cases}}\)
Tọa độ (P) và (d): A(3; 9) và B(-1; 1)
b) Để (P) và (d) cắt nhau tại 2 điểm phân biệt <=> \(\Delta>0\)
<=> (-m)2 - 4.1(-3) > 0
<=> m2 + 12 > 0 \(\forall m\)
Ta có: \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{3}{2}\)
<=> 2x2 + 2x1 = 3x1x2
<=> 2(x2 + x1) = 3x1x2
Theo viet, ta có: \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=m\\x_1x_2=\frac{c}{a}=-3\end{cases}}\)
<=> 2m = 3(-3)
<=> 2m = -9
<=> m = -9/2