Có Tam giác ABC btết góc A = 50o . Tính B, C, biết góc C-góc B = 20o
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 6 2017
A B C H D x
Xét \(\Delta\)ABC: ^CAx là góc ngoài của tam giác ABC => ^CAx=^ABC+^ACB=500+200=700 => ^CAx=700.(1)
Xét\(\Delta\)AHC: ^AHC=900 => ^HAC+^ACH=900 => ^HAC=900-^ACH=900-200=700 =>^HAC=700 (2)
Từ (1) và (2) => ^CAx=^HAC=700 => AC là phân giác của góc ^HAx (3)
Có HD là phân giác của ^AHC (4)
Mà HD giao AC tại điểm D (5)
Từ (3); (4) và (5) => BD là phân giác của ^ABH (Tính chất phân giác trong và 2 phân giác ngoài của tam giác)
=> ^ABD=^HBD=^ABC/2=500/2=250. Vậy ^HBD=250.
25 tháng 11 2016
VD: tên Δ là ABC
Xét ΔABC cân tại A
Nên góc B = góc C= 50o
Ta có: Â + B+ C= 180o
A+ 50o+ 50o=180o
 =180o-(50o+50o)
 =80o
b) Xét Δ ABC cân tại A
Ta có: Â + B + C = 180o
70o+B + C= 180o
B + C=180o- 70o
B +C= 110o( mà B= C)
Suy ra: B = C= 110o:2= 55o
c)Xét ΔABC cân tại A
Ta có: Â + B + C =180o
Ao + B + C= 180o
B+ C=180o- Ao ( mà B= C)
Suy ra: B= C= 180o- Ao:2
(Chú thích: Ao: a độ)
25 tháng 11 2016
a) góc ở đỉnh bằng 80 độ
b) góc ở đáy bằng 55 độ
c) số đo góc B và góc C = (180 - góc A): 2
CM
19 tháng 2 2018
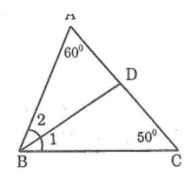
Trong ΔABC ta có:
∠A + ∠B + ∠C = 180o(tổng ba góc trong tam giác)
⇒∠B = 180o - (∠A +∠C )
⇒x = 180o - (60o + 50o) = 70o
(∠B1) =(∠B2 ) = (1/2 )∠B (vì BD là tia phân giác)
⇒ ∠B1 = ∠B2 = 70o : 2 = 35o
Trong ΔBCD ta có ∠(ADB) là góc ngoài tại đỉnh D
⇒ ∠(ADB) = ∠(B1 ) + ∠C (tính chất góc ngoài tam giác)
Nên ∠(ADB) = 35º + 50º = 85º
+) Do ∠(ADB) + ∠(BDC) = 180o(hai góc kề bù)
⇒∠(BDC) = 180o-∠(ADB) = 180o - 85o = 95o
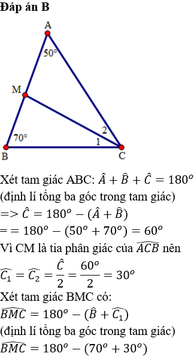
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác ABC ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà \(\widehat{A}=50^o\)nên \(\widehat{B}+\widehat{C}=180^o-50^o=130^o\)
Vì \(\widehat{B}+\widehat{C}=130^o;\widehat{C}-\widehat{B}=20^o\)
Suy ra \(\widehat{B}=\left(130^o-20^o\right):2=55^o\)
Khi đó \(\widehat{C}=75^o\)