1 otô đi từ A đến B với vân tốc xác định. Nếu vận tốc giảm 10 km thì thới gian đến B tăng 45p. Nếu vận tốc oto tăng 10kmthì thời gian đến B giảm 30p. Tính vận tốc thời gian dự định đi của oto
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 12 2018
Gọi vận tốc của oto là x (km/h), x > 15 và thời gian đi từ A đến B của oto là y (h), y > 1
Vậy quãng đường AB là: xy (km)
Nếu vận tốc tăng thêm 30 km/h thì thời gian đi sẽ giảm 1 giờ. Vậy quãng đường AB là: (x + 30)(y - 1) (km)
Nếu vận tốc giảm bớt 15 km/h thì thời gian đi tăng thêm 1 giờ. Vậy quãng đường AB là: (x - 15)(y + 1)
Vậy ta có hệ phương trình:
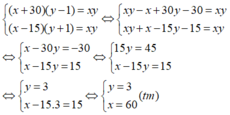
Vậy vận tốc của oto là 60 (km/h) và thời gian oto đi từ A đến B là 3 (h)
24 tháng 2 2021
Gọi a(giờ) và b(km/h) lần lượt là thời gian và vận tốc dự định(Điều kiện: a>0; b>0)
Vì khi ô tô tăng vận tốc lên 8km/h thì đến B sớm hơn 1h nên ta có phương trình:
\(\left(a-1\right)\left(b+8\right)=ab\)
\(\Leftrightarrow ab+8a-b-8=ab\)
\(\Leftrightarrow8a-b=8\)(1)
Vì khi ô tô giảm vận tốc 4km/h thì đến B chậm hơn dự định 40 phút nên ta có phương trình:
\(\left(a+\dfrac{2}{3}\right)\left(b-4\right)=ab\)
\(\Leftrightarrow ab-4a+\dfrac{2}{3}b-\dfrac{8}{3}=ab\)
\(\Leftrightarrow-4a+\dfrac{2}{3}b=\dfrac{8}{3}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}8a-b=8\\-4a+\dfrac{2}{3}b=\dfrac{8}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8a-b=8\\-8a+\dfrac{4}{3}b=\dfrac{16}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{3}b=\dfrac{40}{3}\\8a-b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=40\\8a=8+b=48\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=40\end{matrix}\right.\)(thỏa ĐK)
Vậy: Thời gian dự định là 6 giờ
Vận tốc dự định là 40km/h
AH
Akai Haruma
Giáo viên
22 tháng 12 2021
Lời giải:
Gọi vận tốc dự định là $a$ km/h
Thời gian dự định: $\frac{AB}{a}$ (giờ)
Thời gian khi tăng vận tốc 8km/h: $\frac{AB}{a+8}$ (giờ)
Thời gian khi giảm vận tốc 4km/h: $\frac{AB}{a-4}$ (giờ)
Ta có:
\(\left\{\begin{matrix}
\frac{AB}{a}-\frac{AB}{a+8}=1\\
\frac{AB}{a-4}-\frac{AB}{a}=\frac{2}{3}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
\frac{8AB}{a(a+8)}=1\\
\frac{4AB}{a(a-4)}=\frac{2}{3}\end{matrix}\right.\)
\(\Rightarrow \frac{2(a-4)}{a+8}=\frac{3}{2}\) (chia 2 pt cho nhau theo vế)
$\Rightarrow a=40$ (km/h)
$AB=\frac{a(a+8)}{8}=\frac{40.48}{8}=240$ (km)
Thời gian dự định: $\frac{AB}{a}=\frac{240}{40}=6$ (giờ)
18 tháng 1 2021
Gọi x ( km/h ) là vận tốc dự dịnh của ô tô và y ( giờ ) là thời gian dự định đi của ô tô . ĐK : ( x , y > 0 )
Nếu vận tốc ô tô giảm 10 km/h thì thời gian tăng 45 phút nên ta có phương trình : ( x - 10 )( y + \(\dfrac{3}{4}\)) = xy ⇔ xy + x\(\dfrac{3}{4}\) - 10y - \(\dfrac{15}{2}\) = xy
⇔ \(x\dfrac{3}{4} - 10y = \dfrac{15}{2}\) (1)
Nếu vận tốc của ô tô tăng 10 km/h thì thời gian giảm 30 phút nên ta có phương trình : ( x + 10 )( y - \(\dfrac{1}{2}\) ) = xy ⇔ - \(\dfrac{-1}{2}x\) + 10y = 5 (2)
Từ (1) và (2) ta có hpt giải ra dc x vs y
2 tháng 2 2020
Gọi vận tốc dự định của ô tô là x (km/h)
thời gian dự định là y (h)
Đk x > 10; y > 1
Quãng đường AB là xy (km)
Nếu vận tốc tăng thêm 20 km/h thì vận tốc xe lúc này là x + 20 km/h
Thời gian giảm 1 h ta có y-1
Ta có pt (x+20)(y-1) =xy (1)
nếu vận tốc giảm 10 km/h thì thì vận tốc xe lúc này là x-10 km/h
Thời gian tăng 1h ta có y+1
Quãng đường AB là (x-10)(y+1)
Ta có pt (x-10)(y+1) =xy (2)
Từ (1) và (2) ta có hệ pt
{(x+20)(y-1) =xy (1)
{(x-10)(y+1) =xy (2)
<=>{x-20y=-20
{x-10y=10
<=>{10y=30
{x-10y=10
<=>{y=3 (tmđk)
{x=40 (tmđk)
Vậy vận tốc dự định của ô tô là 40 km/h
Thời gian dự định là 3 giờ
NN
2 tháng 2 2020
Gọi vận tốc dự định của ô tô là x ( km/h ) ( x > 0 )
thời gian dự định của ô tô là y ( giờ ) ( y > 0 )
Quãng đường AB là xy
Vận tốc ô tô khi tăng thêm 20km/h là: x + 20
Thời gian ô tô đi hết quãng đường là: y - 1
\(\Rightarrow\)( x + 20 ).( y - 1 ) = xy
xy - x + 20y - 20 = xy
- x + 20y = 20 (1)
Vận tốc ô tô khi giảm đi 10km/h là: x - 10
Thời gian ô tô đi hết quãng đường là: y + 1
( x - 10 ).( y +1 ) = xy
xy + x - 10y - 10 = xy
x - 10y = 10 (2)
Từ ( 1 ) và ( 2) ta có hệ phương trình
\(\hept{\begin{cases}-x+20y=20\\x-10y=10\end{cases}\Leftrightarrow\hept{\begin{cases}x=40\\y=3\end{cases}}}\)
Vậy vận tốc dự định của ô tô là 40km/h
thời gian dự định của ô tô là 3 giờ
CM
14 tháng 2 2018
30 phút = 1/2 giờ;
45 phút = 3/4 giờ
Gọi vận tốc dự định của ô tô là x (km/h) và thời gian dự định đi của ô tô là y (giờ)
Điều kiện : x > 10; y > 1/2
Lúc đó quãng đường đi của ô tô từ A đến B là x.y (km/h)
Vì ô tô tăng vận tốc lên 10 km/h thì đến B trước 30 phút nên ta có phương trình:
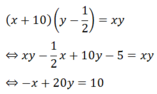
Vận tốc ô tô giảm đi 10 km/h thì đến B chậm hơn 45 phút nên ta có phương trình:
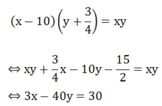
Ta có hệ phương trình
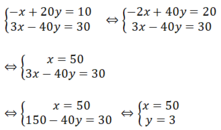
Vậy vận tốc dự định đi của ô tô là 50km/h và thời gian dự định đi của ô tô là 3 giờ.
Lời giải:
Đổi 45'=0,75h và 30'=0,5h
Gọi vận tốc ban đầu là $a$ (km/h) và thời gian đi quãng đường là $b$ (giờ)
Độ dài quãng đường AB là:
$AB=ab = (a-10)(b+0,75)=(a+10)(b-0,5)$
$\Rightarrow ab=ab+0,75a-10b-7,5=ab-0,5a+10b-5$
$\Rightarrow 0,75a-10b=7,5$ và $-0,5a+10b=5$
$\Rightarrow a=50; b=3$
Vậy vận tốc dự định là 50 km/h, thời gian dự định là 3h
Đổi 45 phút = 0,75 giờ; 30 phút = 0,5 giờ; Gọi vận tốc ban đầu, thời gian ban đầu lần lượt là: \(x\) (km/h); t (giờ); \(x\) > 0; t > 0,5
Thì vận tốc lúc tăng, thời gian đi hết quãng đường với vận tốc tăng đó lần lượt là: \({}\)
\(x\) + 10 (km/h); t - 0,5 (giờ)
Và vận tốc lúc giảm; thời gian đi hết quãng đường với vận tốc giảm đó lần lượt là: \(x\) - 10 (km/h); t + 0,75 (giờ)
Do cùng một quãng đường vận tốc tỉ lệ nghịch với thời gian nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{x+10}{x}=\dfrac{t}{t-0,5}\left(1\right)\\\dfrac{x-10}{x}=\dfrac{t}{t+0,75}\end{matrix}\right.\) cộng vế với vế ta có: \(\dfrac{t}{t-0,5}\) + \(\dfrac{t}{t+0,75}\)= 2
⇒ 1 + \(\dfrac{0,5}{t-0,5}\)+ 1 - \(\dfrac{0,75}{t+0,75}\) = 2 ⇒\(\dfrac{0,5}{t-0,5}\)=\(\dfrac{0,75}{t+0,75}\)
⇒ 0,5.(t + 0,75) = 0,75.(t - 0,5) ⇒ 0,5t + 0,375 = 0,75t - 0,375
⇒ 0,75t - 0,5t = 0,375 + 0,375 ⇒ 0,25t = 0,75 ⇒ t = 3;
Thay t = 3 vào (1) ta có: \(\dfrac{x+10}{x}\) = \(\dfrac{3}{3-0,5}\) = 1,2
⇒ \(x\) + 10 = 1,2\(x\) ⇒ 1,2\(x\) - \(x\) = 10 ⇒ 0,2\(x\) = 10 ⇒ \(x\) = 10: 0,2 = 50
Kết luận:...