cho hình thang abcd đường thảng d // với 2đáy và cắt 2 cạnh bên ad,bc tại m,p cắt đườ chéo bd tại n chứng minh ràng dm/da =cp/cb ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AM}{AD}\left(1\right)\)
Xét ΔBDC có ON//DC
nên \(\dfrac{ON}{DC}=\dfrac{BN}{BC}\left(2\right)\)
Xét hình thang ABCD có MN//AB//CD
nên \(\dfrac{AM}{MD}=\dfrac{BN}{NC}\)
=>\(\dfrac{MD}{AM}=\dfrac{CN}{NB}\)
=>\(\dfrac{MD+AM}{AM}=\dfrac{CN+NB}{NB}\)
=>\(\dfrac{AD}{AM}=\dfrac{CB}{BN}\)
=>\(\dfrac{AM}{AD}=\dfrac{NB}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{OM}{DC}=\dfrac{ON}{DC}\)
=>OM=ON

a: DN/BD=DM/DA
CP/CA=CQ/CB
mà DM/DA=CQ/CB
nên DN/BD=CP/CA
b: Xét ΔDAB có MN//AB
nên MN/AB=DM/DA
Xet ΔCAB có PQ//AB
nên PQ/AB=CQ/CP
mà DM/DA=CQ/CP
nên MN=PQ

Trong ΔDAB, ta có: OM // AB (gt)
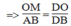 (Hệ quả định lí Ta-lét) (1)
(Hệ quả định lí Ta-lét) (1)
Trong ΔCAB, ta có: ON // AB (gt)
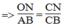 (Hệ quả định lí Ta-lét) (2)
(Hệ quả định lí Ta-lét) (2)
Trong ΔBCD, ta có: ON // CD (gt)
Suy ra: ![]() (định lí Ta-lét) (3)
(định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra: 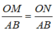
Vậy: OM = ON