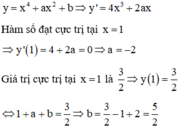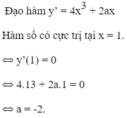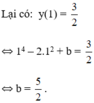Đề bài
Tìm a,b để hàm số y=x4+ax2+b. Tìm a,b để hàm số có cực trị bằng 32 khi x=1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sử dụng giả thiết và điều kiện cần của cực trị ta có
y(1) = 0; y'(-1) = 0; y(-1) = 0
Trong đó , y ' = 3 x 2 + 2 a x + b
Từ đó suy ra:
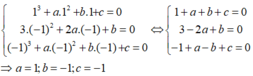
Với a = 1; b = -1; c = -1 thì hàm số đã cho trở thành y = x 3 + x 2 - x - 1
Ta có y ' = 3 x 2 + 2 x - 1 , y ' ' = 6 x + 2 . V ì y ' ' = ( - 1 ) = - 4 < 0 nên hàm số đạt cực đại tại x = -1 . Vậy a = 1; b = -1; c = -1 là các giá trị cần tìm.
Chọn đáp án C.

Đáp án D
Đặt g ( x ) = x 4 - a x 2 - b , ta thấy x = 0 ⇒ y = - b < 0 nên điểm cực đại ở dưới trục hoành và y ' = 4 x 3 - 2 a x = 0 có ba nghiệm phân biệt g(x) sẽ có đồ thị như đồ thị hình bên.
Đồ thị của hàm số g ( x ) = x 4 - a x 2 - b , là phần nằm phía dưới trục hoành và hai nhánh phía trên trục hoành.
Đồ thị của hàm số y = | x 4 - a x 2 - b | có được bằng cách lấy phần phía dưới trục hoành đối xứng qua trục hoành kết hợp với phần ở trên trục hoành. Đó chính là tất cả phần đồ thị trên trục hoành.
Dựa vào đồ thị => Hàm số y = | x 4 - a x 2 - b | có 5 cực trị.

Chọn D.
Ta có CT nhanh 32a3(S0)2 + b5 = 0
Theo công thức suy ra 32.(4√2)2 + (-2m)5 = 0 ⇔ m = 2