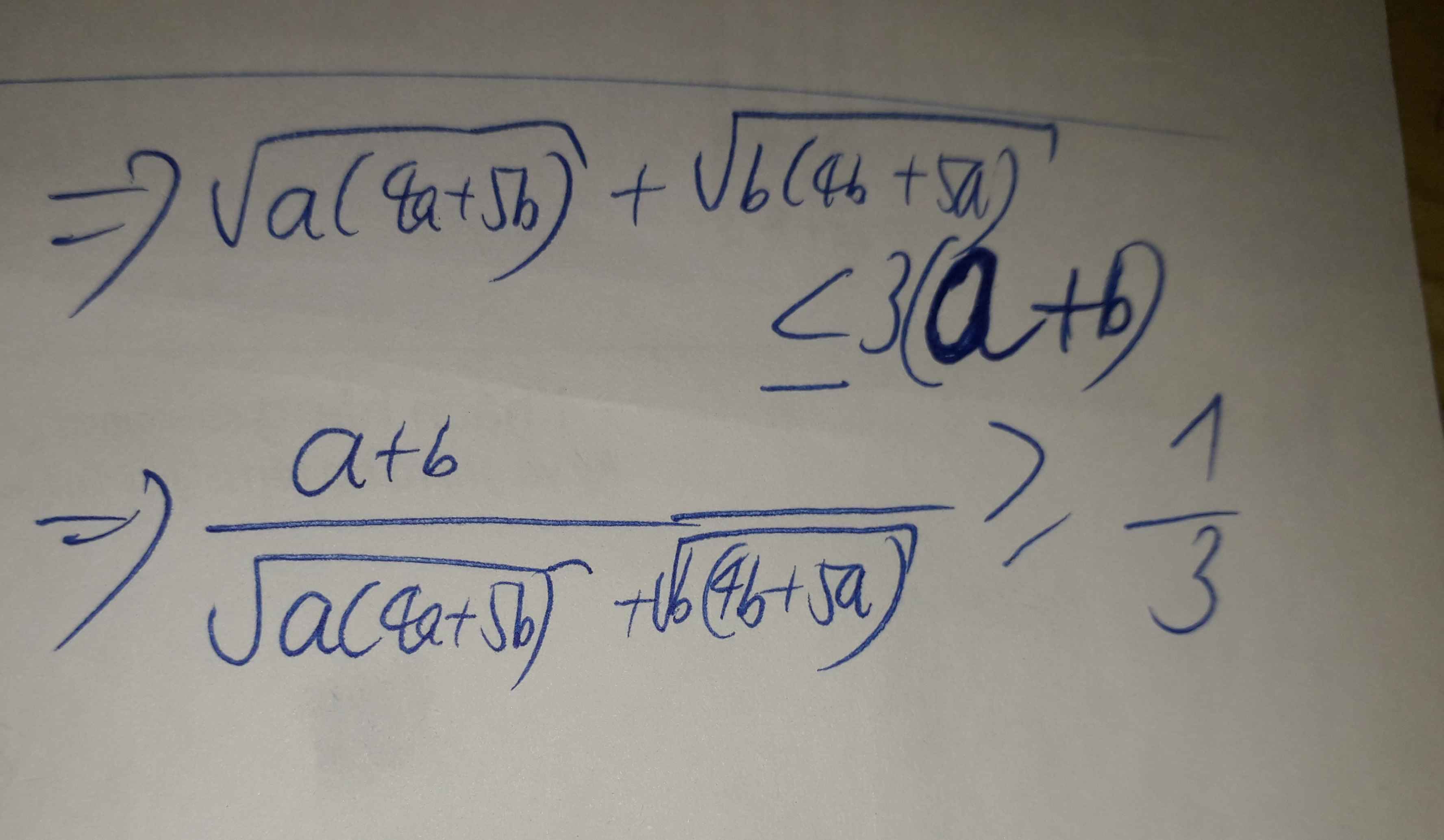cho a,b,c >0 và \(a^2+b^2=2\) tìm GTLN của M = \(a\sqrt{9b\left(4a+5b\right)}+b\sqrt{9a\left(4b+5a\right)}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
14 tháng 5 2021
2M\(\le\)a(9b+4a+5b)+b(9a+4b+5a) (AM-GM)
=4(a2+b2)+28ab\(\le\)4(a2+b2)+14(a2+b2) (AM-GM)
=36 (do a2+b2=2)
=> M \(\le\)18
Dấu bằng có <=> a=b=1
TL
30 tháng 9 2018
Áp dụng BĐT Cô-si cho 2 số không âm
Ta có: \(\sqrt{9b\left(4a+b\right)}\)\(\le\) \(\dfrac{9b+4a+5b}{2}\)=\(\dfrac{14b+4a}{2}\)
\(\Rightarrow\) \(a\sqrt{9b\left(4a+5b\right)}\)\(\le\) \(\dfrac{14ab+4a^2}{2}\)=7ab+2a2
CMTT: \(b\sqrt{9a\left(4b+5a\right)}\) \(\le\) 7ab+2b2
\(\Rightarrow\) M\(\le\) 14ab + 2(a2+b2) \(\le\)7(a2+b2) + 2(a2+b2) = 9(a2+b2)=18
Vậy Mmin=18
Dấu "=" xảy ra\(\Leftrightarrow\) a=b=1
E
30 tháng 9 2018
\(M=a\sqrt{9b\left(4a+5b\right)}+b\sqrt{9a\left(4b+5a\right)}\le\dfrac{a\left(9b+4a+5b\right)}{2}+\dfrac{b\left(9a+4b+5a\right)}{2}=\dfrac{a\left(14b+4a\right)+b\left(14a+4b\right)}{2}=2a^2+7ab+7ab+2b^2=2\left(a^2+b^2\right)+14ab=4+14ab\le4+14\times\dfrac{a^2+b^2}{2}=4+14=18\)
Dấu "=" xảy ra <=> a = b = 1
15 tháng 10 2016
Ta có \(2=a^2+b^2\ge2ab\)
\(\Leftrightarrow ab\le1\)
\(M\le\sqrt{\left(a^2+b^2\right)\left(36ab+45b^2+36ab+45a^2\right)}\)
\(=\sqrt{2\left(72ab+90\right)}\)\(\le\sqrt{2\left(72+90\right)}=\sqrt{324}=18\)
GTLN là 18 đạt được khi a = b = 1
5 tháng 12 2017
\(P=\frac{3\left(a+b\right)}{\sqrt{9a\left(4a+5b\right)}+\sqrt{9b\left(4b+5a\right)}}\)
\(\ge\frac{3\left(a+b\right)}{\frac{9a+4a+5b}{2}+\frac{9b+4b+5a}{2}}=\frac{1}{3}\)
LV
5 tháng 12 2017
Ta có :
\(P^1=\frac{a+b}{\sqrt{a\left(4a+5b\right)}+\sqrt{b\left(4b+5a\right)}}.\)
\(\Leftrightarrow P^2=\frac{3\left(a+b\right)}{\sqrt{9a\left(4a+5b\right)}+\sqrt{9b\left(4b+5a\right)}}\)
Mà ta thấy biểu thức \(P^2\ge\frac{3\left(a+b\right)}{\frac{9a+4a+5b}{2}+\frac{9b+4b+5a}{2}}\)
\(=\frac{1}{3}\)
Vậy giá trị nhỏ nhất của biểu thức \(P=\frac{1}{3}\)
\(\)
NM
1
BN
3 tháng 8 2019
Áp dụng bđt bunhicopxki ta có:
\(\left(\sqrt{a\left(4a+5b\right)}+\sqrt{b\left(4b+5a\right)}\right)^2\le\left(a+b\right)\left(4a+5b+4b+5a\right)=9\left(a+b\right)^2\)
=> \(\sqrt{a\left(4a+5b\right)}+\sqrt{b\left(4b+5a\right)}\le3\left(a+b\right)\)
=>\(P\ge\frac{a+b}{3\left(a+b\right)}=\frac{1}{3}\)
dấu "=" xảy ra khi a=b
