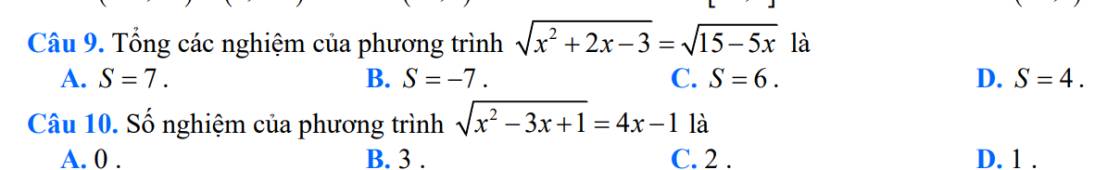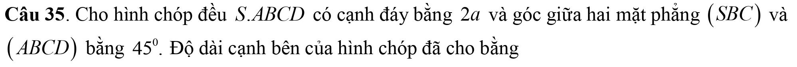cần trình bày câu này ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LD
Lương Đại
24 tháng 12 2023
Đúng(1)
Những câu hỏi liên quan
PH
1
DK
18 tháng 11 2021
“Câu tục ngữ phản ánh mức độ khác nhau trong tình yêu thương vợ chồng. Người con gái luôn luôn thương yêu chồng bằng tình yêu đậm đà, mặn mà, đầy đặn khác nào “đương đông buổi chợ”. Còn tình cảm của người con trai chỉ đôi lúc nhưng mãnh liệt như cái “nắng quái chiều hôm” vậy.
A
18 tháng 11 2021
Tham Khảo
“Câu tục ngữ phản ánh mức độ khác nhau trong tình yêu thương vợ chồng. Người con gái luôn luôn thương yêu chồng bằng tình yêu đậm đà, mặn mà, đầy đặn khác nào “đương đông buổi chợ”. Còn tình cảm của người con trai chỉ đôi lúc nhưng mãnh liệt như cái “nắng quái chiều hôm” vậy. Nắng quái chiều hôm tuy ngắn ngủi nhưng sức nóng, sức cháy bỏng của ánh nắng xiên khoai này thật là ghê gớm”;
12 tháng 4 2017
<=> 7x-1>0 và 3-2x<0 hoặc 7x-1<0 và 3-2x>0
<=> x>1/7 và x>3/2 hoặc x<1/7 và x<3/2
<=> x>3/2 hoặc x<1/7
Vậy với x>3/2 hoặc x<1/7 thì thỏa mãn đề bài
(những chữ "hoặc" và chữ "và" bạn có thể thay bằng dấu ngoặc vuông và ngoặc nhọn nhé!!!)
Have a good day!!!
5N
0
NL
1
19 tháng 6 2023
34:
(SBA) giao (SCD)=d đi qua S, d//AB//CD
=>d vuông góc SA,d vuông góc SD
=>(SAB;SCD)=(SA;SD)
tan ASD=AD/AS=1/căn 3
=>góc ASD=30 độ
H
4 tháng 7 2021
Câu 2 : C
Câu 3 : A
Câu 4 : C
Câu 5 : C
Câu 6 : B
Câu 7 : C
Câu 8 : D
Câu 9 : B
4 tháng 7 2021
Câu 2: C
Pt\(\Leftrightarrow\left\{{}\begin{matrix}x-2\ge0\\x^2+5x-2=\left(x-2\right)^2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\9x=6\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\x=\dfrac{6}{9}\end{matrix}\right.\)\(\Rightarrow x\in\varnothing\)
Câu 3: A
\(\Delta:3x+4y-11=0\)
\(d_{\left(M;\Delta\right)}=\dfrac{\left|3.1+4.-1-11\right|}{\sqrt{3^2+4^2}}=\dfrac{12}{5}\)
Câu 4: Ko có đ/a
Do \(\dfrac{\pi}{2}< \alpha< \pi\Rightarrow tan\alpha< 0;cot\alpha< 0;cos\alpha< 0\)
\(1+cot^2\alpha=\dfrac{1}{sin^2\alpha}\)\(\Rightarrow cot\alpha=\dfrac{-\sqrt{21}}{2}\)
Câu 5:C
Câu 6:B
Câu 7: A
Có nghiệm khi \(\left(m;+\infty\right)\cup\left[-2;2\right]\ne\varnothing\)
\(\Leftrightarrow m< 2\)
Câu 8:D
Câu 9: B
\(cos2\alpha=2cos^2\alpha-1=-\dfrac{23}{25}\)
Câu 10:D
L
1
24 tháng 10 2021
\(\dfrac{2}{7}\cdot\dfrac{14}{15}\cdot\dfrac{5}{6}:\dfrac{3}{8}:\dfrac{2020}{2021}\)
\(=\dfrac{2}{7}\cdot\dfrac{14}{15}\cdot\dfrac{5}{6}\cdot\dfrac{8}{3}\cdot\dfrac{2021}{2020}\)
\(=\dfrac{14}{7}\cdot\dfrac{5}{15}\cdot\dfrac{8}{6}\cdot\dfrac{2}{3}\cdot\dfrac{2021}{2020}\)
\(=2\cdot\dfrac{1}{3}\cdot\dfrac{4}{3}\cdot\dfrac{2}{3}\cdot\dfrac{2021}{2020}\)
\(=\dfrac{8084}{13635}\)
1 tháng 11 2021
Câu 20:
Ta có: \(\widehat{A}-\widehat{B}=40^0\Rightarrow\widehat{B}=\widehat{A}-40^0\)
\(\widehat{A}=2\widehat{C}\Rightarrow\widehat{C}=\frac{\widehat{A}}{2}\)
Vì AB//CD (gt) \(\Rightarrow\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)\(\Rightarrow\widehat{D}=180^0-\widehat{A}\)
Tứ giác ABCD \(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\Rightarrow\widehat{A}+\left(\widehat{A}-40^0\right)+\frac{\widehat{A}}{2}+\left(180^0-\widehat{A}\right)=360^0\)
Và đến đây bạn dễ dàng tìm được góc A và từ đó suy ra được góc D.
1 tháng 11 2021
Câu 29: Ta có:
\(\hept{\begin{cases}xy+x+y=3\\yz+y+z=8\\xz+x+z=15\end{cases}}\Leftrightarrow\hept{\begin{cases}xy+x+y+1=4\\yz+y+z+1=9\\xz+x+z+1=16\end{cases}\Leftrightarrow}\hept{\begin{cases}x\left(y+1\right)+\left(y+1\right)=4\\y\left(z+1\right)+\left(z+1\right)=9\\x\left(z+1\right)+\left(z+1\right)=16\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x+1\right)\left(y+1\right)=4\\\left(y+1\right)\left(z+1\right)=9\\\left(z+1\right)\left(x+1\right)=16\end{cases}}\)
Đặt \(\hept{\begin{cases}x+1=a\\y+1=b\\z+1=c\end{cases}}\)với a,b,c > 1, khi đó ta có
\(\hept{\begin{cases}ab=4\\bc=9\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}abbc=4.9\\c=\frac{9}{b}\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}16b^2=36\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b^2=\frac{36}{16}=\frac{9}{4}\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b=\frac{3}{2}\\c=\frac{9}{\frac{3}{2}}=6\\a=\frac{16}{6}=\frac{8}{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=a-1=\frac{8}{3}-1=\frac{5}{3}\\y=b-1=\frac{3}{2}-1=\frac{1}{2}\\z=c-1=6-1=5\end{cases}}\)
Vậy \(P=x+y+z=\frac{5}{3}+\frac{1}{2}+5=\frac{10+3+30}{6}=\frac{43}{6}\)
NL
3
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
15.
\(\Delta'=m^2+m-2>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -2\end{matrix}\right.\)
Đáp án B
16.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow\dfrac{\pi}{4}< \dfrac{a}{2}< \dfrac{\pi}{2}\Rightarrow\dfrac{\sqrt{2}}{2}< sin\dfrac{a}{2}< 1\Rightarrow\dfrac{1}{2}< sin^2\dfrac{a}{2}< 1\)
\(sina=\dfrac{3}{5}\Leftrightarrow sin^2a=\dfrac{9}{25}\Leftrightarrow4sin^2\dfrac{a}{2}.cos^2\dfrac{a}{2}=\dfrac{9}{25}\)
\(\Leftrightarrow sin^2\dfrac{a}{2}\left(1-sin^2\dfrac{a}{2}\right)=\dfrac{9}{100}\Leftrightarrow sin^4\dfrac{a}{2}-sin^2\dfrac{a}{2}+\dfrac{9}{100}=0\)
\(\Rightarrow\left[{}\begin{matrix}sin^2\dfrac{a}{2}=\dfrac{1}{10}< \dfrac{1}{2}\left(loại\right)\\sin^2\dfrac{a}{2}=\dfrac{9}{10}\end{matrix}\right.\)
\(\Rightarrow sin\dfrac{a}{2}=\dfrac{3\sqrt{10}}{10}\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
17.
Áp dụng công thức trung tuyến:
\(AM=\dfrac{\sqrt{2\left(AB^2+AC^2\right)-BC^2}}{2}=\dfrac{\sqrt{201}}{2}\)
18.
\(\Leftrightarrow x^2+2x+4>m^2+2m\) ; \(\forall x\in\left[-2;1\right]\)
\(\Leftrightarrow m^2+2m< \min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)\)
Xét \(f\left(x\right)=x^2+2x+4\) trên \(\left[-2;1\right]\)
\(-\dfrac{b}{2a}=-1\in\left[-2;1\right]\) ; \(f\left(-2\right)=4\) ; \(f\left(-1\right)=3\) ; \(f\left(1\right)=7\)
\(\Rightarrow\min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)=f\left(1\right)=3\)
\(\Rightarrow m^2+2m< 3\Leftrightarrow m^2+2m-3< 0\)
\(\Rightarrow-3< m< 1\Rightarrow m=\left\{-2;-1;0\right\}\)
Đáp án C