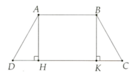
Cho hình thang cân ABCD ( AB// CD , AB < CD ) có AH là đường cao. C/m DH=(CD-AB)÷2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 8:
a: Xét ΔDBC có
E là trung điểm của BD
M là trung điểm của BC
Do đó: EM là đường trung bình của ΔDBC
Suy ra: EM//DC
b: Xét ΔAEM có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM
Bài 5:
Xét ΔABC có
\(\dfrac{AE}{EB}=\dfrac{AD}{DC}\left(=1\right)\)
Do đó: DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân

a) Chứng minh
DADH = DBCK (ch-gnh)
Þ DH = CK
Vận dụng nhận xét hình thang ABKH (AB//KH) có AH//BK Þ AB = HK
b) Vậy D H = C D − A B 2
c) DH = 4cm, AH = 3cm; SABCD = 30cm2

Xét ΔAHD và ΔBKC có:
\(\widehat{AHD}=\widehat{AKC}=90\left(gt\right)\)
AD=BC(gt)
\(\widehat{D}=\widehat{C}\left(gt\right)\)
=>ΔAHD=ΔBKC (cạnh huyền-góc nhọn)
=>DH=CK


Xét tam giác AHD vuông tại H và tam giác BKC vuông tại K
Ta có: AD= BC (gt)
Góc D = góc C
=> tam giác AHD= tam giác BKC (cạnh huyền- góc nhọn)
=> DH= CK ( 2 cạnh tương ứng)
xét tam giác AHD và tam giác BKC có:
AD = BC (gt)
góc ADH = góc BCK (gt)
góc AHD = góc AKC = 900
=> tam giác ... = tam giác .... (ch-gn)
=> DH = CK (cạnh tương ứng)
t i c k nha!! 463745768658897697696789768568654

xét tam giác ADH và BCK
góc H= góc K =90 độ
AD=BC(tính chất hình thang cân)
góc D =góc C(tính chất hình thang cân)
=>tam giác ADH=tam giác BCK(cạnh huyền - góc nhọn)
=>DH=CK
A B C D H K
Xét \(\Delta\)ADH và \(\Delta\)BCK
có AD=BC vì (ABCD là hình thang cân nên có 2 cạnh bên = nhau)
\(\widehat{D}=\widehat{C}\) (ABCD là hình thang cân nên có 2 cạnh bên = nhau)
\(\widehat{AHD}=\widehat{DKC}=90^o\)
Nên \(\Delta\)ADH và \(\Delta\)BCK(Cạnh huyền góc nhọn)
suy ra DH=CK(2 cạnh tương ứng)
quá dễ
xét 2tam giác vuông AED và BFC có
AD=BC
gD=gC
=>tam giác AED=BFC(cạnh huyền - góc nhọn)
=>DE=CF(2 cạnh tương ứng)
k mk nhé