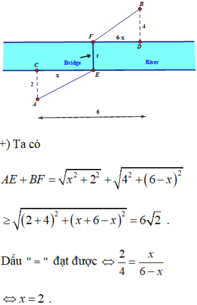
giá cây cầu AB bắc qua một con sông có chiều rộng 300m .Người ta chọn điểm E trên đường thẳng AB sao cho điểm E,C,D thẳng hàng.Trên mặt đất người ta đo được AE=400m EC=500m tính khoảng cách giữa C và D
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:
\(\dfrac{{A{\rm{E}}}}{{AB}} = \dfrac{{CE}}{{C{\rm{D}}}}\) hay \(\dfrac{{400}}{{300}} = \dfrac{{500}}{{C{\rm{D}}}}\)
Suy ra \(C{\rm{D}} = \dfrac{{300.500}}{{400}} = 375\) (m).
Vậy khoảng cách giữa C và D bằng 375 m
22 tháng 6 2023
Xét ΔCAB có FE//AB
nên FE/AB=CF/CA
=>6/AB=4/10=2/5
=>AB=15(m)
1 tháng 2
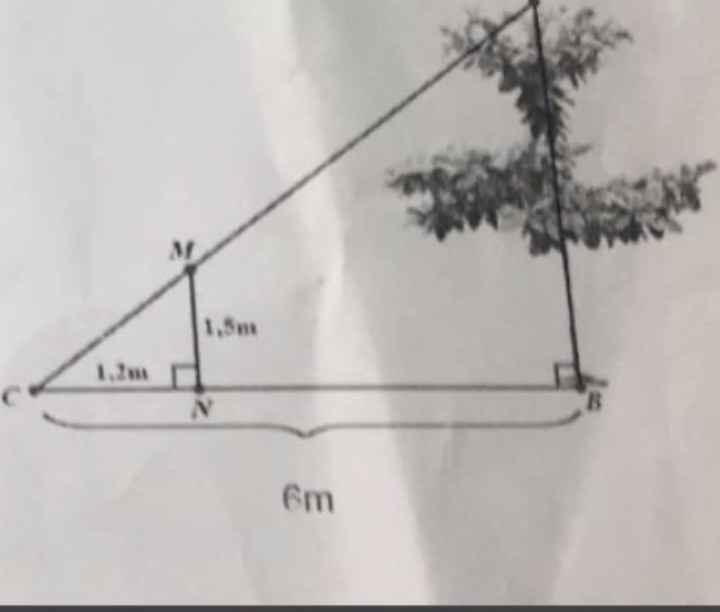
Ta có:MN\(\perp\)CB
AB\(\perp\)CB
Do đó: MN//AB
Xét ΔCAB có MN//AB
nên \(\dfrac{MN}{AB}=\dfrac{CN}{CB}\)
=>\(\dfrac{1.5}{AB}=\dfrac{1.2}{6}=\dfrac{1}{5}\)
=>AB=1,5*5=7,5(m)
18 tháng 12 2023
Xét ΔCAB có FE//AB
nên \(\dfrac{CF}{FA}=\dfrac{CE}{EB}\)
=>\(\dfrac{30}{EB}=\dfrac{20}{40}=\dfrac{1}{2}\)
=>\(EB=30\cdot2=60\left(m\right)\)
14 tháng 5 2021
Ta có: NM//AB
=> \(\dfrac{NM}{AB}=\dfrac{CN}{AC}< =>AB=1,5\cdot\dfrac{20}{1,25}=24\left(m\right)\)
Vậy tòa nhà đó cao 24m
25 tháng 4 2023
a: AE=AC=10/2=5cm
BE+AB=AE
=>BE=3cm
b: BC=2+5=7cm
c: DE=10-4=6cm
BE và BD là hai tia đối nhau
=>B nằm giữa E và D
mà EB=1/2*ED
nên B là trung điểm của ED
11 tháng 6 2021
Ta có :
\(\dfrac{NM}{AB}\) và \(\dfrac{CN}{CA}\) .
Vì \(\dfrac{NM}{AB}\) = \(\dfrac{CN}{CA}\) \(\Leftrightarrow\) AB = 1,5 . \(\dfrac{20}{1,25}\) = 24 ( m ) .
Vậy chiều cao AB của tòa nhà đó là 24 m .