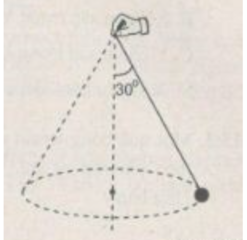
Một vật nặng có kích thước nhỏ, có khối lượng 0,50 kg, được buộc vào đầu một dây có chiều dài 1,5 m. Vật chuyển động đều trên đường tròn nằm ngang (Hình 21P.2). Cho biết dây chỉ chịu được lực căng tối đa bằng 50 N. Hãy tính tốc độ quay lớn nhất của vật để dây không bị đứt.
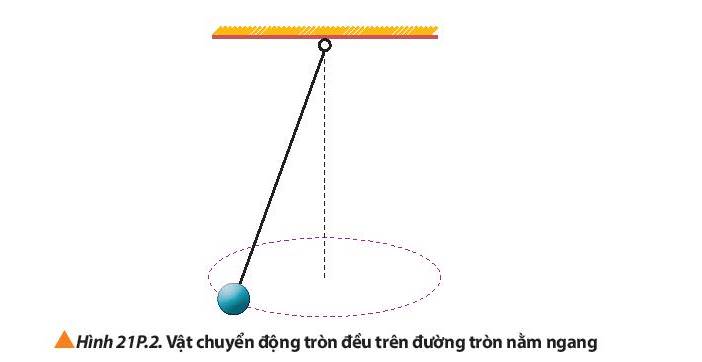

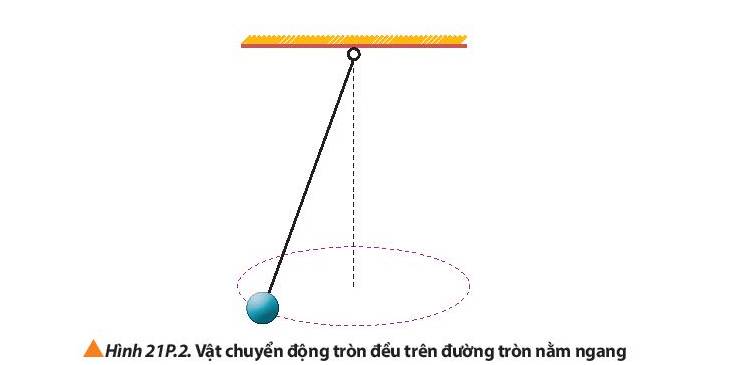


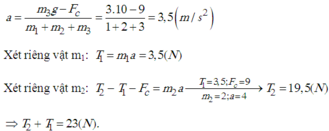
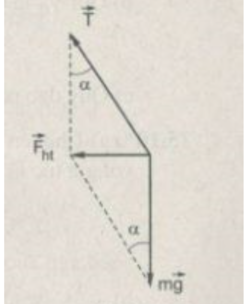
Lực đóng vai trò là lực hướng tâm trong trường hợp trên là lực căng.
=> Vận tốc cực đại của vật để dây không bị đứt là:
\(\begin{array}{l}{T_{\max }} = {F_{ht\max }} = m.\frac{{v_{\max }^2}}{R}\\ \Rightarrow {v_{\max }} = \sqrt {\frac{{{T_{\max }}.R}}{m}} = \sqrt {\frac{{50.1,5}}{{0,5}}} \approx 12,23(m/s)\end{array}\)